倒三角形高强钢可移动桥梁极限承载力影响因素分析研究*(建筑)
高 磊 江克斌 何晓晖 白林越
(中国人民解放军理工大学野战工程学院,南京210007)
摘 要:倒三角形高强钢可移动桥梁是一种新型桁架结构体系,因此有必要对其整体稳定性进行深入的研究。基于已有的BS700高强钢材料性能试验,提出了有限元模型使用的材料模型。建立了51 m跨度桥梁的有限元模型,并与实桥加载试验进行了对比,验证了有限元模型的精确性。在综合考虑材料和几何双重非线性的基础上,进行桥梁的非线性屈曲分析,得到桥梁的极限承载力和稳定安全系数。然后对影响桥梁极限承载能力的因素进行分析,分析结果表明:上弦杆、桥梁高度是影响桥梁极限承载力的重要因素,其中上弦杆1的影响最大;车辙宽度、下弦杆和斜腹杆对桥梁极限承载力影响较小,直腹杆的影响略大于斜腹杆的影响。
关键词:倒三角形;高强钢;非线性屈曲分析;极限承载力;影响因素
DOI:10. 13206/j.gjg201605006
1概述
日本、美国等国家已经在较多的建筑工程实例中采用了屈服强度在460~690 M Pa之间的高强钢,同时在一些可移动桥梁中用到1 100 M Pa级别的超高强钢。近几年国内也出现了越来越多的高强钢建筑,主要采用Q420和Q460两种高强钢。采用高强钢材料能有效降低结构自重,节约成本。在我国可移动桥梁中也大量使用高强度的钢材,倒三角形高强钢可移动桥梁是利用高强钢BS700(名义屈服强度700 M Pa)研制的一种新型大跨度桥梁。桥梁单跨长度达51 m,由两片倒三角形桁架结构组成两个车辙(每个车辙承载整车半边车轮,车辙之间空置以减轻重量),两个车辙之间在上部用强横梁连接成整体,桥梁由6个桥节组成,典型的桥节组成如图1所示。此种桥梁主要用于抗震救灾、交通应急保障等多个领域,具有可移动、拼装迅速、承载力大等多种优点。为了减轻重量便于桥梁移动,采用高强钢材料BS700。
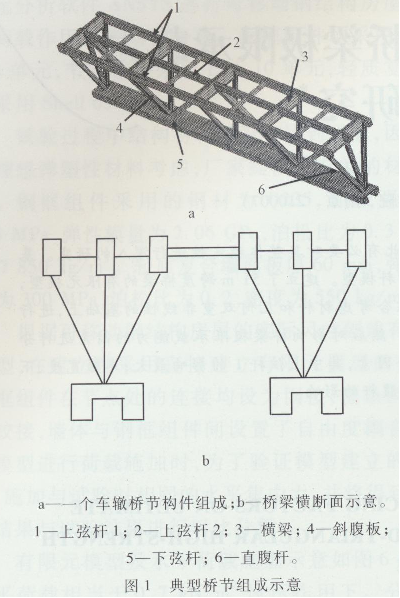
目前国内外常用的桁架桥,都是一种采用类似“箱形”截面的桁架体系,此种桁架体系以辅助联接系,在横截面上组成一个近似半刚性的框架结构,稳定问题不是非常突出。随着大跨度空间结构的发展,出现了一种倒三角形的桁架体系作为屋架结构使用,为了保证其稳定性在横向没置很多联接系。而本文研究的倒三角形高强钢可移动桥梁是一种车辙式桥梁,车辙宽度仅为1.125 m,长度51 m,为了便于机械化架设下弦所以没有设置联接系,同时采用了高强钢降低整桥重量,使得整桥重量低于承受的荷载。
研究桁架桥稳定性最常用的方法是将其连续化为可变形的薄壁箱形截面梁,利用薄壁箱形截面梁的相关稳定理论开展研究,但只能研究弹性阶段的稳定性。随着弹塑性理论的不断成熟,对于桁架桥的侧倾稳定问题开始考虑几何和材料的非线性,已经由弹性屈曲分析阶段转到了非弹性屈曲分析阶段。相关的方法有二阶分析法、广义增分法、非线性欧拉理论等,近几年随着有限元理论的发展,越来越多的学者开始采用有限元方法研究桁架结构的稳定性问题。本文基于非线性屈曲的相关理论,综合考虑了结构材料、几何双重非线性,对倒三角形高强钢可移动桥梁的稳定性展开研究,得到了桥梁的极限承载力,并对影响其承载力的因素进行了研究。
2极限承载力分析有限元模型
2.1 非线性分析的相关理论
特征值屈曲分析只能得到结构弹性阶段理想的承载能力,通常数值比较大,只能定性地分析结构的承载能力,无法真实的反应结构的承载能力,为此需要对结构进行非线性屈曲分析。非线性屈曲分析也称为极值点失稳或结构的第二稳定性,能考虑结构的几何缺陷、材料非线性等因素,因此更能真实反映结构的承载能力。在结构的非线性分析中主要包含材料非线性和几何非线性。
当考虑了材料和几何双重非线性之后,屈曲的基本方程为:

2.2 有限元模型的建立
采用有限元软件ANSYS 12.0进行有限元分析,单元采用Beam 189,此单元可以使用自定义截面。建模时基于APDL语言采用参数化建模,整个有限元模型分为基本模型、特征值屈曲分析、缺陷引入、非线性屈曲分析、结果处理5个模块。建模时考虑实际使用情况在桥梁两端各留出1 m作为支撑,故桥梁实际跨度为47 m,为了分析方便不考虑桥面板的作用,建立的有限元基本模型如图2所示:
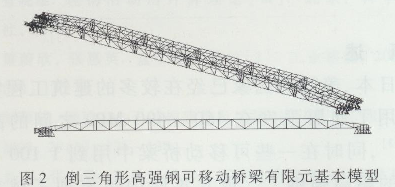
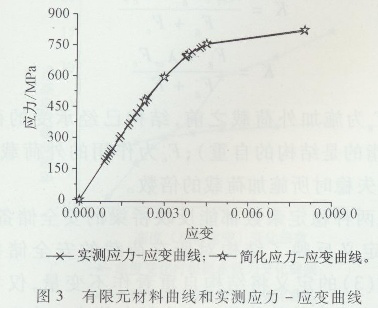
建立基本模型时考虑材料的非线性,采用Mises屈服准则和随动强化准则。基于已有的高强钢材料BS700实测材料应力-应变曲线,进行简化并提出本文需要的材料本构关系曲线。模型中认为材料是均质的,没有内部缺陷,各项同性,据此在有限元模型中采用多线性随动强化模型。简化的曲线和实测的曲线对比如图3所示。
对于几何缺陷的考虑,采用一致缺陷模态法。一致缺陷模态法就是用最低阶屈曲模态来模拟结构的最不利几何缺陷的分布。为此首先对整桥进行特征值屈曲分析,得到一阶屈曲模态下桥梁的最大位移8max,在此基础上乘以一定的系数,用UPGEOM命令引入到基本模型中,控制施加的最大初始缺陷为桥梁最大跨度的1/1 000。
2.3 有限元基本模型的验证
建立的倒三角形高强钢可移动桥梁基本有限元模型能否准确反映桥梁的实际受力情况是关系到有效计算桥梁极限承载力的关键,为此进行了试验验证。试验采用实桥堆载形式进行,试验施加的最大荷载超过了桥梁设计承载力(履带600 k N),以此来检验桥梁的承载能力。
分别在两端(L/6,5L/6,L为桥梁跨度)和跨中( L/2)布置了3个挠度测点,并布置了多个应变测点。加载时利用吊车吊装钢板缓慢加载,现场加载示意如图4所示。结构的整体稳定性与刚度密切相关,为此对桥梁挠度的实测结果和有限元数值计算结果进行详细分析,如表1所示。其中,由于测试之前自重的挠度已经完成,没有测量,所以测点的挠度只考虑荷载作用产生的挠度。

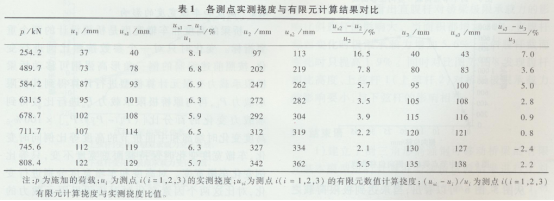
从表1可以看出对于3个测点除第一级荷载外其余的差别大都在6%左右。在荷载为254.2k N时3个测点实测值与有限元计算值差别较大,主要原因在于拼装式结构有很大的连接间隙,虽然在自重下完成了部分变形,但加载之后连接处的非线性变形才会逐渐完成,需要一定的时间。同时实测的挠度都比有限元模拟的数值略大,主要原因在于实际测量时,桥梁内部有架设用的导梁,当荷载作用后,主梁变形后与导梁接触,此时导梁会发挥一定作用,增大了主梁的刚度。而有限元数值模拟时没有考虑导梁的作用,这样有限元得到的计算结果偏大。总之,除去一些客观不利因素影响,建立的倒三角形拼装桁架桥有限元模型较精确地模拟了实际桥梁。
3 桥梁的极限承载力分析
在建立了倒三角形高强钢可移动桥梁基本有限元模型的基础上,综合考虑材料和几何非线性,利用弧长法非线性屈曲分析求解。非线性稳定分析的基本方法是逐步地施加一个恒定的载荷增量直到求解变得开始发散为止。以承受履带荷载600 k N为基础进行特征值屈曲分析,得到其屈曲荷载,此荷载是桥梁屈曲荷载的上限。通常将此荷载扩大10%~20%作为非线性屈曲的给定荷载,在渐进加载达到此荷载前,非线性求解应该发散。通过时间通用后处理器( Post 26),借助弧长法追踪桥梁在荷载逐步增加过程中的荷载一位移曲线,曲线的最高点即表示达到了桥梁的极限承载力,此时的时间参数就是极限荷载对应的荷载系数,用此系数乘以施加的荷载得到桥梁实际承受的荷载。通过计算得到的47 m跨度桥梁的极限承载力为1637.6 kN,得到跨中的荷载一位移曲线如图5、图6所示。
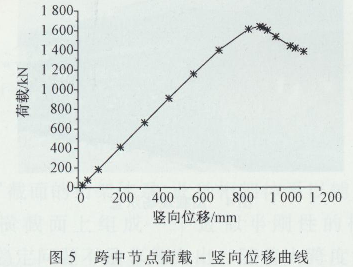
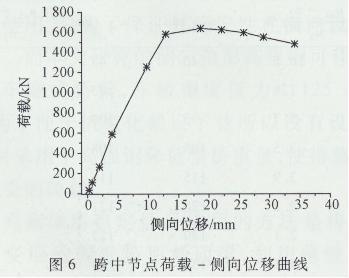
从图5、图6可以看出,当未达到极限荷载之前,跨中节点的荷载一位移曲线基本呈线性变化,竖向位移较大而侧向位移很小,说明桥梁呈现的是面内竖向弯曲。但一旦到达极限荷载之后,荷载一位移曲线呈现非线性变化,桥梁侧向位移变大,桥梁呈现竖向弯曲和侧向扭转同时发生的弯扭屈曲,桥梁丧失了承受荷载的能力。
当得到了结构的极限承载能力,为了评估结构的稳定安全性,需要界定合理的评估方法,通常采用稳定安全系数加以量化。针对结构的非线性屈曲分析,当前对于其稳定安全系数有两种定义。,分别如式(2)、式(3)所示:

此两种稳定系数都能反映桥梁的安全储备,式(2)的定义反映了结构对所有荷载的安全储备能力。式(3)的定义将结构自重看作不变量,仅考虑结构除自重之外的荷载的安全储备能力。本文在极限承载能力分析时,没有考虑结构的自重,因此采用式(3)来定义结构的稳定安全系数。通过计算得到安全系数为2. 11。
4极限承载力的影响因素分析
影响倒三角形高强钢可移动桥梁整体稳定性的因素有很多,涉及到桥梁设计的主要有桥梁的跨度、高度、车辙宽度和各个截面的大小等。为了研究各个因素对桥梁整体稳定性的影响大小,进行了大量计算,得到了各个参数变化对桥梁稳定承载力影响的大小。
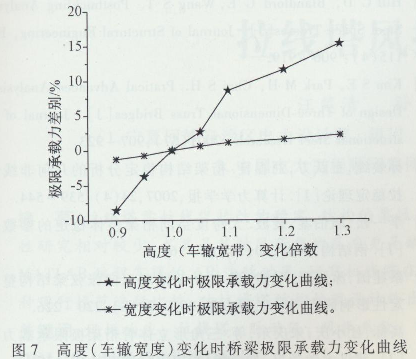
4.1 高度和车辙宽度的影响
桥梁的高度和车辙宽度是桥梁设计的两个重要指标。变化时只对一个参数按照比例进行变化,按照前述编制的倒三角形高强钢可移动桥梁极限承载力有限元计算模型进行计算得到其极限承载力P b,再与原桥极限承载力P u进行比较得到承载力变化的百分比[(P b –P u)/P u]×100%。高度变化时端部和中间桥节的高度等比例同时变化,车辙宽度变化时保持截面总宽度不变,只等比例变化车辙宽度。对高度和车辙宽度分别进行变化,对比这两个因素变化时对桥梁极限承载力的影响如图7所示。
从图7可以看出高度对倒三角形高强钢可移动桥梁的极限承载能力的影响要比宽度大。比如当高度增加30%时,极限承载力增加15. 3%,而当车辙宽度增加30%时,极限承载力仅增加2.1%。分析原因:主要在于当高度增加时截面的抗弯刚度增加,桥梁抗弯极限承载力增加。而在总体宽度不变的情况下,只改变两个车辙的宽度,对桥梁抗扭刚度的增加不大,所以极限承载力变化不大。
4.2 弦杆的影响
倒三角形高强钢可移动桥梁的上、下弦杆是桥梁最重要的杆件,为此分别研究了上弦杆和下弦杆变化时对极限承载能力的影响。上弦杆1和上弦杆2都是一种箱形截面,变化时截面高度和宽度等比例的变化,不断调整比例系数使得截面面积达到要变化的倍数。对于下弦杆是一种复杂的组合截面,主要控制几个主要尺寸,使其等比例的变化,同样不断调整比例系数使下弦杆的面积变化达到要变化的倍数。通过分析计算得到弦杆变化时桥梁极限承载力的变化对比如图8所示。
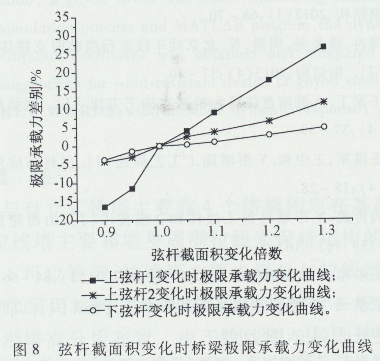
从图8可以看出上弦杆对极限承载力的影响比下弦杆的影响大。两种上弦杆,上弦杆1的影响比上弦杆2的影响大,对比图7还可以发现上弦杆1的影响比高度的影响还要大。当面积都增加30%时,上弦杆1的变化能提高极限承载力26.6%,上弦杆2可以提高11.6%,而下弦杆仅提高4.8%。分析后发现,原因主要在于桥梁承受荷载时上弦杆受压,受压杆件容易失稳,桥梁整体极限承载力与单个杆件的极限承载力密切相关。同时,如图1所示,上弦杆1位于车辙板宽度的两侧,提供的抗扭惯矩比上弦杆2提供的大,所以同是上弦杆件,上弦杆1对极限承载力的影响比上弦杆2大。下弦杆处于受拉侧,对桥梁整体极限承载力的贡献较小。
4.3腹杆的影响
腹杆在桁架桥中主要起抗剪的作用,但也提供一定的抗弯和抗扭刚度,因此也研究了腹杆变化时对极限承载力的影响。根据图1所示桥节结构有两种不同的腹杆,截面都为箱形截面,采用同上弦杆截面变化相同的方法改变腹杆的截面积,研究其对极限承载能力的影响,结果如图9所示。
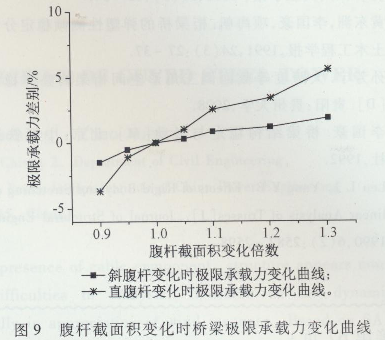
从图9可以看出直腹杆对桥梁极限承载力的影响比斜腹杆的影响大。当面积都增加30%,直腹杆截面变化时极限承载力增加5. 6%,而斜腹杆截面变化时只提高1. 9%。同时对比图7、图8发现腹杆相比高度、上弦杆1(上弦杆2)对桥梁极限承载力的影响要小,与下弦杆的影响相当。
5 结束语
1)建立了倒三角形高强钢可移动桥梁的有限元基本模型进行计算并与实桥试验结果进行了对比,验证了建立的有限元模型可靠。综合考虑了材料和几何双重非线性,得到47 m跨度桥梁的极限承载力为1637.6 kN,稳定安全系数为2.11。
2)研究了影响桥梁极限承载力的各种因素,研究发现上弦杆截面积大小、桥梁高度是影响桥梁极限承载力的重要因素,其中上弦杆1的影响最大。
3)车辙宽度、下弦杆和腹杆截面积对桥梁极限承载力的影响不大。相比之下直腹杆截面积对桥梁极限承载力的影响大于斜腹杆截面积的影响。