通风网络分支风量与风机频率及变频灵敏度的关系研究*(安全)
韩 靖1,2,蒋曙光2,王媛媛2,樊 尧2,胡利明2,苗磊刚1
(1.安徽理工大学能源与安全学院,安徽淮南2320011;2.中国矿业大学安全工程学院,江苏徐州221116)
摘要:为了定量描述主要通风机变频调风时通风网络风量变化的差异性,推导了分支风量随频率变化的函数关系式,表明分支风量与风机频率呈一次函数关系,依此可以精准高效地进行变频调风,并预判待调分支是否满足调风要求以及对非待调分支风量变化的影响。提出了变频灵敏度的概念,定量地反映了通风网络各分支风量相对于频率变化的敏感程度,其值可用风量与频率函数的斜率表征。通过理论推导可知变频灵敏度与分支风量具有相同的数值分
布规律,得出风量越大的分支在变频调风时风量改变量也越大的结论。分析了所述理论对矿井变频调风工作的指导作用,并通过矿井变频调风时的风网解算验证了理论的正确性。
关键词:通风网络;风量;频率;风机;变频调风;变频灵敏度;Q-f函数
中图分类号:X936 doi: 10. 11731/j. issn.1673 -193x.2016. 05. 005
0 引言
近年来,众多学者对井下风量调节进行了大量研究,发现风阻调节很难实现风量的定量、精确调控。随着变频技术的引入,变频调风具有操作方便简单、自动化程度高、快速、高效、实时、定量、精准调节风量的优点,已被部分矿井应用于实践。但目前矿井风机变频调节的理论分析主要侧重内部原理和节能分析,关于分支风量随频率变化关系方面的理论鲜有研究,而风量一频率关系的研究可有效预估调风效果,避免盲目调频,实现精准高效调风,具有较大意义,基于此,文中以理论和风网解算的形式对其进行初步研究。
在变频调风实验中,发现各分支风量的变化值呈现差异性,不同分支对频率响应的敏感程度不同,且存在部分分支风量“调不动”及部分分支风量“超调”的情况,为了合理使用变频调风,需要研究变频调风时的不同分支风量变化的敏感程度,以此可有效发挥不同敏感程度分支的价值,解决变频调风时盲目调频的现象。目前,国内外对变频调风的敏感性鲜有研究,文中基于灵敏度的定义结合风量一频率函数对此进行初步研究。
近年来,有学者基于变频调风提出了防灭火和瓦斯防治的方法,这对矿井具有较大意义,本文的研究所提供的风量与频率的函数关系及变频灵敏度将有助于推动变频调风在灾变防治中的应用。
1 网络分支风量与风机频率
目前大多数矿井风机采用异步电动机拖动,异步电动机的转速与频率的关系为:
由流体力学相似定律可知,风机风量Q与转速n之间的关系为:

在保持磁极对数和异步电动机转差率不变的情况下,由式(1)和式(2)联立可推导出风量和频率的对应关系:

由式(3)可以看出,风机的风量Q与频率f呈正比变化,设其变化函数关系为式(4):
![]()
式中:k为风量变化斜率,k值与风机结构、尺寸、电动机、叶片等风机固有属性有关,与电动机频率无关,风机制造完成后,在不改变上述参数的情况下,其k值不变,因此k值在一定程度上能够反映风机的调风能力。
在矿井通风中,矿井总风量即风机的风量Q,当f=0时,风机处于无电状态,由式(4),风量等于0,而在矿井自然风压的作用,矿井风量值不为0,因此式(4)不成立,为使式(4)在矿井变频调风中进行应用,需将式(4)进行自然风压修正,修正式为式(5),其中6为在自然风压驱动下的风量,将其称为自然风量。



2 变频灵敏度
变频调风时,风机频率的改变会使得总风量发生改变,进而使得通风网络各分支风量发生改变,由于不同分支固有属性和所处的风网位置不同,各分支风量变化相对于频率变化不同,部分分支风量相对于频率的变化较大,而部分分支对风量的变化较小。为了定量研究这种风量变化的差异性,提出变频灵敏度的概念。
根据灵敏度的一般定义,当对主要通风机的频率施加一个极小的频率变化量![]() 时,任一分支j的风量变化
时,任一分支j的风量变化

由式(10)知,变频灵敏度与k i互等,求得k i值便可求得分支的变频灵敏度,因此,分支与 k i值可反映分支风量对调频响应的敏感程度,具有不同k i值的分支,则其风量变化灵敏度不同;变频灵敏度与频率无关,所调频率的大小对变频灵敏度无影响。同时,式(10)也为变频灵敏度的求解提供了一种方法。
3 变频灵敏度数值分布
变频灵敏度k i反映的是i分支风量变化量的大小,当i值发生变化时,k i值也随之发生变化,即不同分支变频灵敏度数值分布呈现差异性。对k i值分布情况进行研究有助于提前知悉各分支的变频灵敏度,进而为变频调风作参考。
将式(8)进行变形得式(11),各分支的变频灵敏度符合式(11):

现研究频率f固定不变时,各分支变频灵敏度k i随分支不同的分布情况。由式(11)可知,各分支的变频灵敏度k i为各分支风量Q i和自然风量bi的函数。风机动力大于自然风压动力,分支间自然风量bi的差异量相对于总风量Q i的差异量很小,可以忽略,所以分支风量Q i大的分支,其变频灵敏度k i值也较大,反之则越小。由此可见,矿井各分支变频灵敏度的分布等同于各分支风量分布。各分支的风量分布由各分支风阻、分支所处的风网位置等有关,因此,可印证各分支变频灵敏度也受分支风阻、分支所处风网位置等的影响。
4 Q-f函数及变频灵敏度对矿井变频调风的指导作用
1)Q-f函数的精准调节和预判断作用
以此函数为基础,可实现风量的精准调节,避免盲目调频,可提高调风效率;可预先算出达到期望风量所需的频率值,并判断该频率是否超过风机的最大频率,若超过最大频率,则风量无法调至期望风量;预先将期望频率代入其他非待调分支的Q-f函数关系式中,计算出各分支在该频率下的风量,以此可预判变频调风对非待调分支风量的影响程度。
2)指导巷道布置或巷道调整
若待调节分支k i值较大,变频调风时此类分支风量变化明显,能淋漓尽致的发挥出变频调节优势;若非待调节分支k i值较大,变频调风时会出现待调节分支的风量变化不明显,而非待调节分支风量变化明显的情况,这将失去调风的意义,这种情况不可取。因此,在变频调风时,为有效发挥变频调风优势,则应使非待调节分支为k i值较小的分支,待调分支为k i值较大的分支。
新建矿井在巷道布置或已建矿井遇到调风问题需进行巷道调整时,可采用合理的方法使经常调风的分支k i值较大,使不经常调风或要保持分支风量稳定的分支成为k i值较小的分支。
3)通过增阻或减阻的方法达到较好的调风效果
一些重要的且需要经常调风的分支,可通过减阻的方法将其设置为大风量分支。由变频灵敏度和风量具有相同的数值分布可知,大风量分支的变频灵敏度也较大,有利于调风。对于一些不需要经常调风且风量又较大的分支,其他分支变频调风时,为使其影响值降至最小,可针对此类分支的部分分支进行增阻调节,降低其变频灵敏度,减少有害影响。
4)调风失败诊断
在变频调风时,若出现风量“调不动”或风量“超调”的情况,则视为调风失败,可从风量与频率函数关系、变频灵敏度方面分析调风失败的原因。风量“调不动”可能是由于其变频灵敏度较小或者所调频率值没有达到计算的期望频率值;风量“超调”可能是由于其变频灵敏度较大或者所调频率值超过了计算的期望频率值。
5 验证与分析
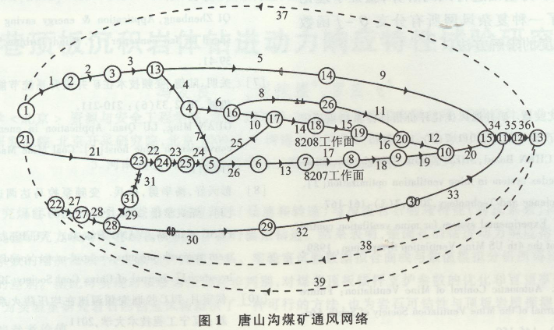
因矿井变频调风涉及到整个矿井所有通风网路风量的变化,对整个通风网路的风量在多个频率下进行测量会耗费极大的人力物力,为此,以唐山沟煤矿为例,采用唐山沟煤矿的基础数据,以风网解算的方法进行研究,通风网络图见图1。
以唐山沟煤矿的风机在27、29、31、33、35 Hz频率下的5条风机特性曲线信息(含推算曲线)为基准,将这5个频率下的风机特性曲线各参数和各分支的风阻值带入风网解算程序,即可得到5个不同频率下的各个分支的风量信息,其中,三个分支的风量进行现场测量校验,误差范围较小。以频率为横坐标,以风量为纵坐标,可作出各分支风量随频率的变化图像,如图2。
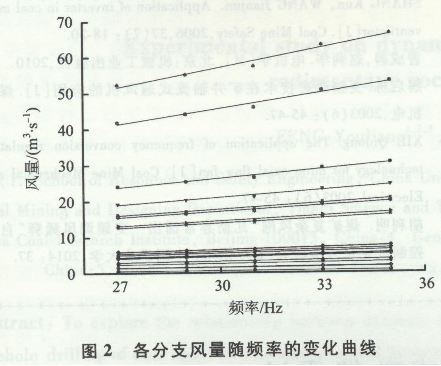
由图2可得以下结论:
1)Q-f函数线性拟合效果较好,验证了Q-f函数理论的正确性,依斜率可看出变频灵敏度大小,依截距可看出自然风压的大小。
2)部分分支风量变化较小甚至不变,如5、9、8号分支等;而部分分支风量变化较为明显,如35、36、37号等分支。反映了变频调风时,不同分支风量的变化大小存在差异,相对于频率改变时各分支风量变化的敏感程度不同。
3)提供了一种求分支Q-f函数的方法。矿井通风网络复杂,部分矿井分支数达数百条之多,对于此类矿井,对通风网络各个分支进行Q-f函数的测量不太现实,因此,可以采用不同频率的风机特性曲线与风网解算配合的方法。
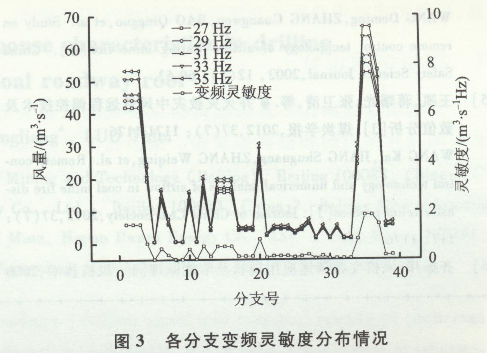
以分支号为横坐标,以不同频率下各分支风量和变频灵敏度的分布情况为纵坐标进行作图,得图3。
由图3可看出,各分支的变频灵敏度和各分支在所选27~35 Hz下的风量分布情况严格一致,符合上文对变频灵敏度分布情况的描述,同时也说明了风量越大的分支其变频灵敏度越大,风量越小的分支其变频灵敏度越小。
6 结论
1)由频率与转速的关系及风量与转速的关系,结合自然风压修正,推导出了Q-f函数,结果表明分支风量与风机频率呈一次函数关系。以此函数为基础,可实现精准的风量调节,避免盲目调频,提高调风效率,且可预判待调分支是否满足调风要求及对非待调分支风量变
化的影响情况。
2)提出了变频灵敏度的概念,其值可用风量与频率函数关系的斜率表示,其可定量描述风机变频调风时井下不同分支风量变化的敏感程度。通过理论推导得出了变频灵敏度与风量的数值分布具有相同的规律,得出了风量越大的分支在变频调风时越有利于调风的结论,为矿井变频调风工作提供一定的指导作用。
3)以唐山沟煤矿为基础进行风网解算,验证了理论的正确性,并提供了一种复杂风网所有分支Q-f函数及各分支变频灵敏度的求解方法。