不同设计基准期桥梁结构可靠指标的动态分析

 冷福增  王潮海  郑继光

(1．吉林建筑大学交通科学与工程学院长春130118；

2．吉林省交通运输厅长春130025；

 3．吉林省交通科学研究所长春130012)

摘要  基于影响桥梁结构可靠度的基本因素，考虑恒载与汽车荷载效应的基本组合，通过推算汽车荷载在不同设计基准期内的统计参数，采用可靠度校准法对不同设计基准期下桥梁结构的可靠度进行分析。并由JC法计算不同破坏类型受力构件的目标可靠指标值与结构抗力均值。结果表明，目标可靠指标与设计基准期近似呈线性递减关系，不同基准期下达到同一目标可靠指标所需抗力均值与设计基准期近似呈线性递增关系。

关键词  桥梁工程  可靠度  校准法  目标可靠指标  结构抗力  设计基准期

 现行工程结构设计主要采用以概率理论为基础的极限状态设计方法，以保证结构在设计基准期内达到一定的目标可靠指标为准则。为保证结构安全可靠与经济合理，国内外房屋建筑、铁路、公路、港口、水利水电等行业相继制定了可靠度设计标准，对目标可靠指标做了不同规定。不同行业工程结构采用的设计基准期往往不同，如建筑结构是50年，而桥梁结构是100年，结构所采用的目标可靠指标随设计基准期而不同，要使不同设计基准期的结构达到同一目标可靠指标，则结构设计抗力须做相应调整。基于现行公路桥梁设计规范，通过可靠度校准法，对不同设计基准期下桥梁结构的目标可靠指标及达到同一目标可靠指标所需抗力进行分析，可为桥梁结构可靠性评估与加固提供一定的理论基础。

1基本理论

1.1  可靠度分析基本原理

对结构进行可靠度分析时，一般将影响结构可靠度的因素简化为结构抗力与作用效应综合函数，结构的极限状态可采用下列方程描述。

1.2随机过程与截口随机变量

 随机过程是一族依赖于时间t的随机变量的总称，在结构的可靠性分析中，可将荷载及荷载效应随机过程记为{Q(t)，0≤t≤T}。可变荷载所采用的随机过程类型主要依据其任意时点的概率分布类型，在设计基准期[0，T]内，取任意时刻t-t。，t。上一切可能出现的结果可用一个随机变量来描述，这个随机变量叫做截口随机变量，也称为任意时点随机变量，它的分布称为任意时点的概率分布，记为Fm(x)。

1.3  随机变量最大值分布理论

在采用概率极限状态设计方法进行结构设计时，所考虑荷载对应于设计基准期最大荷载，故进行可靠度分析时需将可变荷载随机过程转化为设计基准期内最大值随机变量处理。设有一组互相独立且服从同一概率分布F(z)的随机变量z，，X2，…，z。则它的最大值项XM—max{ Xi，X：，…，XM)也是一个随机变量，称为随机变量的最大值项，其分布函数为

桥梁结构的设计基准期采用100年，本文引用文献[6]中对既有桥梁结构可靠度校准所用分析结果，且仅考虑一般运行状态，其概率分布函数及统计参数为

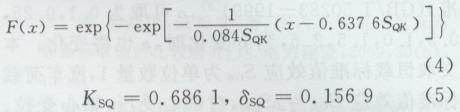
式中：K为随机变量均值系数；d为变异系数，各随机变量的统计参数和概率分布类型以实际观测或模拟试验为基础，获得统计样本，然后通过参数估计和分布优度拟合，最终得出合适的概率分布类型。上述统计结果表明汽车荷载效应服从参数为a，B的极值I型分布，其最大值项的分布函数及其数字特征为

2  基本变量统计参数

2.1  汽车荷载效应统计参数

考虑车辆运行情况的年变化量不会太大，采用平稳二项随机过程来描述汽车荷载随机过程，认为截口分布时段为1年，且发生的概率p=l。由极值I型最大值随机变量的概率特性可知，任意设计基准期内汽车荷载效应最大值的统计参数：

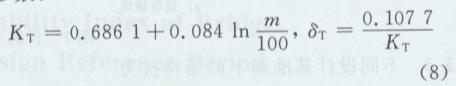
经计算不同设计基准期汽车荷载效应的统计参数见表1。

2.2抗力及恒载效应统计参数

表2为文献[6]中所用抗力及恒载效应的统计参数，其中抗力服从对数正态分布，恒载效应服从正态分布，且二者均不随设计基准期而变化。

3桥梁结构可靠度分析

3.1基本参数

基本变量R，SG，SQ的统计参数可由下式确定。

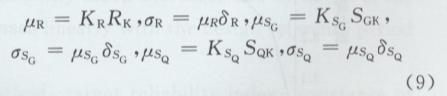
其中抗力标准值为恒载标准值效应SGK与活载标准值效应SQK的线性函数。

在校准可靠指标B时，需考虑可变作用标准值效应与永久作用标准值效应所具有不同的比值fD的情况，根据《公路工程结构可靠度设计统一标准》(GB/T 50283_1999)，p可取为0.1，0.25，0.5，1．O，1.5，2.5，当p变化时，fD也将变化。本文取恒载标准值效应SGK为单位数量1，汽车荷载标准值效应SQK—pSGK，对轴心受压、轴心受拉、受剪、受弯、大偏心受压5种受力构件的可靠度进行分析。

3.2不同设计基准期下的目标可靠指标

当只考虑恒载与汽车荷载组合时，结构的极限状态方程为

式中：R为结构抗力；SG为恒载效应；SQ为汽车荷载效应在设计基准期内的最大值，其中抗力与汽车荷载效应随机变量均不服从正态分布，采用验算点法(JC法)对结构的可靠度进行计算，不同破坏类型构件的计算结果取各受力构件的加权平均值，其中受剪构件取矩形截面与T形截面的平均值。

表3为不同破坏类型受力构件在不同设计基准期下的目标可靠指标，图1为目标可靠指标随设计基准期的近似变化曲线。

3.3不同设计基准期下的结构抗力

 以上对结构可靠度的分析中，均将抗力视为常量，从另一方面考虑，若要使不同设计基准期的构件达到同一目标可靠指标，那么抗力需做出相应调整。按照《公路工程结构可靠度设计统一标准》(GB/T 50283 -1999)规定，取目标可靠指标值为4.2，对结构的可靠度进行逆向运算。

表4为不同破坏类型受力构件在不同设计基准期下目标可靠指标达到4.2时所需的抗力均值，图2为抗力均值随设计基准期的变化曲线，对图1、图2中曲线进行线性拟合分析，结果表明在结构设计基准期为50～100年间，线性相关系数较高。

4结论

 (1)不同破坏类型受力构件的目标可靠指标均随结构设计基准期的增加而减小，不同基准期下达到同一目标可靠指标所需抗力均值随设计基准期增加而增大。

 (2)经过线性拟合分析，设计基准期大于50年时线性相关系数较高，认为目标可靠指标与设计基准期近似呈线性递减关系，不同基准期下达到同一目标可靠指标所需抗力均值与设计基准期近似呈线性递增关系。

 (3)以延性破坏构件为例，设计基准期为50年时，目标可靠指标约为现行目标可靠指标的1. 03倍，可靠度水平偏高，若想使其达到原有的可靠度，则其设计抗力应减小为原参数的0. 98倍，其他设计基准期下可靠度的对应变化关系可按相应线性比例计算。