关于重庆地区中长期负荷特性和预测方法的探索

作者：张毅

     目前．有许多学者对中长期负荷预测方法进行了研究，常规的预测方法有相关分析法、回归分析法、时间序列法等，但通常都是直接建立数学表达式对负荷及相关因素之间的关系进行描述．难以获得较好的预测精度：而灰色预测方法则克服了常规预测法概率统计的弱点，减小了原始数列随机波动性对预测精度的影响．目前最常用的一种灰色模型是GM(1，1)灰色模型，并在中长期负荷预测中得到了广泛的应用．但该模型主要适用于时间短、样本数据少、波动不大的系统对象．当存在多个相互影响或关联的变量时，就无法反映它们之间相互影响、制约和协同发展的情况，冈此在实际应用中有一定的局限。

  为充分利用灰色预测模型的优势．本文提出采用多变量灰色预测模型MGM(1，m)进行中长期负荷预测．它是通过将负荷序列和多个影响因素序列建立m个n元微分方程，通过联立求解使所得的模型参数能满足多变量的相互关系．最终使预测值更符合实际。该模型已在灾害预警和建筑物沉降等预测中获得较好的预测效果。

1  中长期负荷特性分析

  根据收集的重庆地区2004-2014年年用电量负荷数据．绘制出10年来重庆地区用电负荷的发展趋势，如图1所示。

  从图1可知．10年来重庆地区用电量总体呈上升趋势。图2的年用电量相对变化曲线显示2013年增幅最大，其次为2005年和2010年，而2012年和2014年用电量则呈现负增长趋势。这一方面，是2013年电量过大引起：另一方面，可能是影响因素造成。2004-2014年重庆年最大负荷利用小时数曲线如图3所示，在—卜五”前期重庆电网最高负荷增长很快．峰谷差加大，年最大负荷利用小时数逐年降低。2004年以后，电力供应紧张受电网拉闸限电和价格杠杆等需求侧管理手段的影响，最大负荷利用小时数有所增加。2008年以后，供电形势好转，区外来电增加，拉闸限电措施大大减少，使得年最大负荷利用小时数呈减小趋势。为更清楚了解后5年电量变化规律．绘制了2010-2014年每年12个月的用电量变化曲线，如图4所示。

  图4显示．2010-2014年各月用电量变化趋势非常相似，每年的8月为用电高峰。通常8月为重庆全年最高温度，导致降温负荷大幅增加：2月多为用电低谷．因为春节是中国最重要的传统节日．大部分企业因放假而停产导致负荷大大降低，2013年6、7、8月3个月的用电量均较高，造成全年峰谷差加大。

2中长期负荷的影响因素

2.1  经济因素

  用电量来源于重庆市的生活和生产运行需要，在总用电量中居民生活用电仅占很少的部分，即5%左右．其余大多为企业用电．凶此可以用发电量的升降来衡量经济状况。同时，地区经济的发展水平也决定了电力需求的增长速度，经济是电力发展的第一推动力，地区经济发展水平的高低、经济效益的好坏将直接影响电网负荷的变化趋势，图5表示了重庆地区2004-2014年用电量和生产总值的变化曲线。

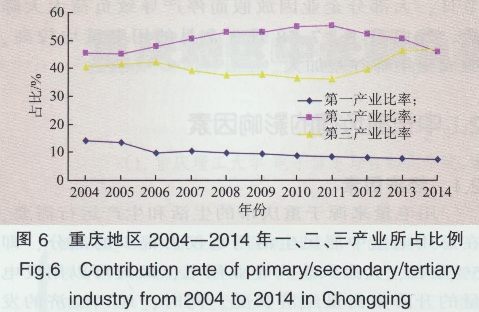
  图5显示，近10年来，重庆地区经济发展一直处于增长势头．用电量与生产总值则有相似的增长趋势．充分展现了总用电量受经济发展的影响程度较大．但在2012年用电量略有下降，从生产总值增幅来看．2011年重庆市GDP增长率为26.3%，在2012年其增长率仅为14.5%．比2011年下降了1 1.8%．从用电结构看．第二产业用电量同比出现小幅下降．尤其工业用电量呈现明显下降趋势。因此，经济的发展和经济结构的调整将影响着电力的变化。在重工业发展过程巾，第二产业经济通常占据着国民经济的主导地位，其用电量占全社会用电量比重处于上升趋势，随着科技发展．作为支柱产业的工业开始向高产低耗型发展模式转变．其用电量所占比重呈现减弱趋势，而第三产业及居民生活用电则大幅增加，如图6所示。

2.2人口与居民生活水平

  电能的产生是为了满足人类生产和生活的需要，人口作为电力需求的重要因素，具有其特殊性，人口越多，其生活用电越多，其生产经营或工作所需的电能供应也较多。随着国民经济的高速发展．居民收入水平和消费观念得到很大改变，因此居民收入及城镇化水平反映了居民生活水平的高低。居民收入及生活水平的提升，对居民生活用电具有极大的推动作用，尤其对家用电器结构的变化产生较大影响．主要通过家用电器的普及程度和使用强度间接反映其对用电需求的影响。图7和图8显示了重庆市2004-2014年总用电量与人口和人均可支配收入的关系曲线。

  图7、图8显示近10年来，重庆市人口一直处于上升趋势．人均可支配收入逐年增加，并与总用电量具有相似的变化趋势。

2.3气温气候

  中国地域辽阔，气温气候差异性大，而且不同地区气温气候对负荷的影响程度也各不相同。重庆位于长江流域上游，气候与其他城市明显不同，属“夏热冬冷”地区，夏季酷暑，冬季湿寒。随着生活水平的提高．具有制冷和制热的空调普及率越来越高．这将造成电力负荷中气温敏感性负荷比重的增加，使得气温气候已成为影响地区负荷的重要因素之一。

  从图5可知．重庆2004-2014年生产总值总体呈现上升趋势．因此2012年用电量下降受生产总值影响不大。图9中2008-2014年每月最高温度显示．2012年6-10月最高温与其余年份相比均处于较低温度值．连续近5个月的舒适温度使得降温负荷得以减少．从而使得全年总负荷较201 1年和2013年低，而在2013年的6、7、8月3个月的最高温度几乎变化不大．使得该年的降温负荷得以增加。比较分析显示，温度对中长期负荷的变化起着重要作用。

2.4政策及其他因素

  政策凶素包括经济政策、经济调控措施、用电政策等．通过一系列政策引导企业（尤其是那些高能耗、高排放行业）和居民在生产和生活中实行节能减排和低碳经济．从而影响了电力负荷增长速度及负荷曲线的变化趋势。除此之外，可再生能源如风能和太阳能等的利用对电力需求也将产生较大影响。

3多变量灰色预测模型

  假设电力负荷数据及其影响因素为Jm维数据序列．每个序列代表系统的一个因素变量的动态行为，且每维数据序列有n个观测数据，即

式中：i=1，2，…，m。对原始数据序列进行一次累加．生成序列为

则可获得MGM(1，m)模型的一阶常微分方程组的形式为

  假设微分方程的初始条件为X(1)=x(0)(1)，且相应矩阵均可逆，利用最小二乘法可求得参数向量ai和bi的估计值。

4中长期电力负荷的多变量灰色预测实例

  由第2节分析可知，巾长期电力负荷影响冈素较多．如果采用常规的单变量灰色预测模型GM(1，1)较难获得满意的预测精度，因此，本文采用常规模型GM(1，1)和多变量灰色模型MGM(1.m)分别进行建模，得出拟合结果进行分析比较。模型数据均来自重庆电网2004-2014年年用电量．而在众多负荷影响因素巾选取主要影响囚素之一的生产总值建立MGM(1，2)预测模型。

  根据收集的重庆2004-2014年重庆生产总值和年用电量数据，应用Matlab仿真软件通过多变量灰色预测模型计算各变量的累加序列X(1)和数据矩阵L,求得拟合参数A和B,从而获得拟合函数．累减还原最终获得预测值。预测结果如表1

所示。为检验预测效果，本文采用残差检验法进行分析和比较。

  从表1和图10预测误差显示，对于常规灰色预测模型GM(1，1)的最大预测误差为-7.65%，

大于5.00%的有5个预测点．平均误差达到4.20%；采用多变量灰色预测模型MGM(1，2)的

最大预测误差为-6.37%．大于5.00%的预测点有2个，平均误差为3.10%．因此采用多变量灰色预测模型MGM(1，2)的精度优于单变量灰色模型GM(1，1)。在2种预测模型中，2011-2014年的预测误差相对较大．是由于该时段用电量变化较大，受其影响因素的影响大，因此要提高中长期负荷的预测精度不得不考虑影响因素的影响。

5结语

根据重庆10年来的年总用电量数据分析可知，中长期电力负荷具有近似指数的变化规律，但由于受经济指标、产业结构、消费观念和气候等多因素的影响，中长期电力负荷特性则呈现出高度的非线性与随机性，从而加大了中长期电力负荷的预测难度。灰色预测法具有要求负荷数据少、不考虑变化趋势、运算方便、易于检验等特点，但常规灰色预测模型GM(1，1)不仅要求预测数据具有指数增长趋势．而且没有充分考虑影响因素的影响，因此本文引入了主要影响因素中的生产总值建立了多变量灰色预测模型MGM(1，2)。与常规灰色预测模型的预测结果比较显示，多变量灰色预测模型具有更好的预测精度。值得指出的是，中长期电力负荷所受影响因素众多，选择合适、有效的因素对提高预测精度具有重要意义。

6摘要：对于存在多个影响因素的中长期电力负荷，采用常规灰色模型GM(1,1)进行中长期预测不能获得较好的预测精度。提取了中长期负荷主要影响因素之一的生产总值和年总用电量建立了多变量灰色预测模型MGM(1，2)。为进行比较分析，同时还建立了常规灰色GM(1,1)模型。预测结果显示，多变量灰色模型MGM(1，2)的预测精度优于常规灰色模型GM(1,1)。