独塔斜拉桥抗震性能分析(交通)
张卫红
(中铁大桥局集团有限公司设计分公司 武汉 430050)
摘要为对特殊桥梁进行抗震分析,以一座72.5 m+62.5 m不等跨预应力混凝土独塔双索面
斜拉桥为工程背景,建立全桥三维空间有限元模型,在动力特性计算基础上,采用地震反应谱多维抗震分析方法,输入不同等级的地震动作用,对结构进行了抗震性能分析。分析采用基于纤维模型的截面弯矩曲率弹塑性分析方法。计算结果表明,该独塔斜拉桥结构在El和E2地震作用下具有良好的整体抗震性能。
关键词 独塔斜拉桥 动力特性 地震反应谱纤维模型 弹塑性分析方法
近年来,我国修建了大量斜拉桥,其中独塔斜拉桥以其明确可靠的受力体系而得到广泛的应用,这些桥梁的抗震性能越来越受到重视。但由于目前关于斜拉桥的抗震研究工作还不够充分,交通部发布的《公路桥梁抗震设计细则》(JTG/T B02-01-2008)(以下简称《细则》)中,对斜拉桥等特殊桥梁只给出了设计原则。为此,国内外许多学者对其展开过深入的理论性研究,并就不同的抗震计算方法给出了实践性指导建议。
笔者依据桥梁抗震设计相关规范,依托工程设计实例,提出了基于纤维模型的弹塑性分析方法,对预应力混凝土独塔斜拉桥采用多振型反应谱法进行基于性能目标的抗震计算分析,为该类桥梁的抗震设计提供参考。
1 工程概况
辽宁省海城市同泽大桥主桥采用72.5 m+62.5 m不等跨预应力混凝土独塔双索面斜拉桥。
斜拉桥主梁采用预应力混凝土变高、变宽箱梁,箱梁采用单箱3室截面,边支点、跨中箱梁中心高2.4 m,在桥塔位置局部加高为3.2 m。主塔柱采用椭圆型外包钢板混凝土结构,塔高自梁顶以上45 m,单个截面横桥向宽度截面为变宽度(塔顶至塔梁固结底面为2.5 m,承台顶为4m),纵桥向宽度截面为变宽度(塔顶为4.0 m,桥面处为5.0 m,承台顶为6m),斜拉索采用直径7 mm的平行钢丝,冷铸锚体系,塔上设张拉端。桥塔下采用2个由系梁连接的承台,承台尺寸为14.4 m×22.0 m×4.5 m。基础采用24根直径2.0 m桩基础。
2有限元模型建立
采用Midas/Civi建立结构空间有限元计算模型。其中主梁、墩柱、桩基均采用空间梁单元模拟。考虑斜拉索垂度效应,并利用节点弹性支撑模拟桩一土相互作用,其顺桥向、横桥向及竖向约束刚度采用m法计算。计算模型见图1。
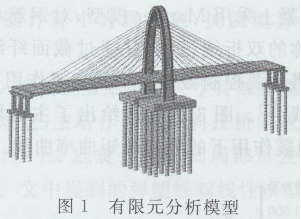
3动力特性分析
按照多自由度结构的自由振动进行特征值分析,将成桥状态前10阶频率及振型列于表1。
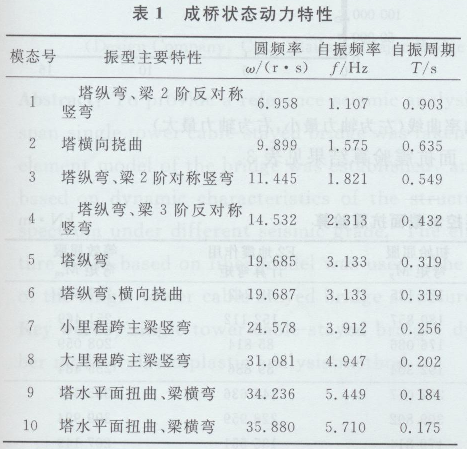
通过计算分析,该独塔斜拉桥体系具有如下动力特性。
(1)由于本斜拉桥为塔梁固接体系,计算结果表明该桥基本周期较短,理论计算值为0. 903 s,反映出该体系的斜拉桥刚度较大的特点。
(2)结构的1阶模态为塔纵弯、梁反对称竖弯,表明主塔在纵向刚度上小于横向刚度,主塔顺桥向地震计算中可能为最不利。但结构在随后发生的2阶模态中即出现塔横向挠曲,说明主塔横桥向地震效应也应该引起重视。
(3)双索面斜拉桥由于拉索能提供抗扭能力,导致结构抗扭刚度增加,扭转频率增大,由计算可知,该桥在第9阶振型中才出现塔水平面扭曲。
4抗震计算分析
4.1分析方法
桥位区地震基本烈度7度,地震动反映谱特征周期为0. 35 s,设计地震峰值加速度为0.15g,工程场地类型为II类。抗震计算中,结构地震响应通过加速度反应谱分析得到,反应谱结果采用《细则》中相关规定。
根据《细则》,本72.5 m+62.5 m独塔斜拉桥为7度区的B类桥梁,应按下列要求进行抗震验算。
(1)在El地震作用下,结构不发生损伤,保持在弹性范围内。
(2)在E2地震作用下,主塔、基础、主梁等重要结构受力构件局部可发生可修复的损伤,地震后基本不影响通行。
地震作用的振型组合采用CQC法;计算地震时考虑2种组合:恒载作用效应十地震作用效应,地震作用效应分别考虑顺桥向X(同时计入竖向Z)和横桥向Y(同时计人竖向Z)的地震作用。
4.2地震力计算结果
主塔抗震计算中控制截面位置示意见图2,鉴于篇幅所限,仅列出E2地震作用下各部位地震力计算结果见表2。
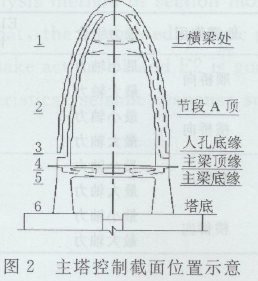
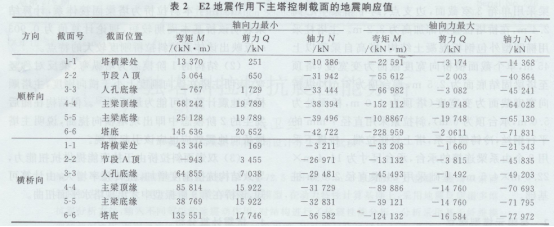
在E1和E2地震作用下,由于考虑到竖向地震作用,因此存在着轴向力最大(竖向地震作用向下)和轴向力最小(竖向地震作用向上)2种情形。
由地震力计算结果可知,在E2顺桥向地震作用下,塔底截面弯矩最大,为228 959 kN.m,梁顶缘塔截面弯矩亦较大,为152 112 kN.m;横桥向地震作用下,塔底截面弯矩为135 551 kN.m,梁顶缘塔截面弯矩为89 886 kN.m。
根据主塔设计方案中的截面配筋及地震效应判断,主要对梁顶缘及塔底2控制截面进行抗震验算。验算按E1地震作用阶段和E2地震作用阶段分别进行。
4.3截面弯矩一曲率分析
《细则》中关于特殊桥梁抗震设计的章节里,提到了将验算截面划分为纤维单元,并通过数值积分法得出弯矩一曲率曲线的计算方法。
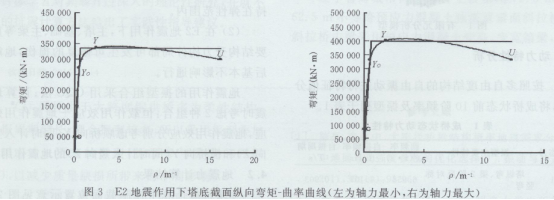
基于此,通过建立合适的弹塑性材料滞后模型,对混凝土采用Mander模型,对钢筋材料采用一般对称的双折线模型,并通过截面纤维划分计算出主塔主要控制截面在不同地震作用下的弯矩曲率曲线。图3示例性给出了主塔塔底截面在E2地震作用下的纵向弯矩曲率曲线。
4.4抗震验算结果
E1及E2地震作用下主塔梁顶缘及塔底截面抗震验算结果见表3。
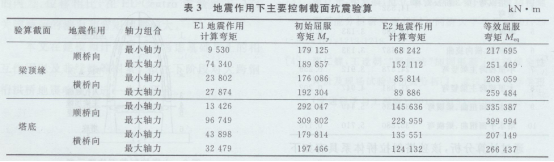
抗震验算结果表明,在E1地震作用下,桥塔截面弯矩小于截面初始屈服弯矩My(考虑轴力)。由于My为截面最外层钢筋首次屈服时对应的初始屈服弯矩,因此当地震反应弯矩小于初始屈服弯矩时,整个截面保持在弹性,结构满足在弹性范围工作的性能目标。
在E2地震作用下,桥塔截面弯矩小于截面等效抗弯屈服弯矩M e q(考虑轴力)。M e q是把实际弯矩一曲率曲线等效为理想弹塑性双线性恢复力模型时得到的等效抗弯屈服弯矩。从理想弹塑性双线性模型看,当地震反应弯矩小于等效抗弯屈服弯矩时,结构整体反应还在弹性范围内。
5结语
(1)由动力特性分析的结果可以看出,海城市同泽大桥主桥采用塔梁固结体系,结构的1阶模态表现为塔纵弯、梁反对称竖弯,塔纵弯先于横弯发生,表明主塔纵向刚度小于横向刚度,主塔顺桥向地震计算中为最不利,抗震验算中证实了此点。
(2)依据抗震细则中关于特殊桥梁抗震设计的有关规定,主塔作为独塔斜拉桥的重要结构受力构件,在E2地震作用下其局部可发生可修复的损伤。文中提到的弹塑性双线性模型等效抗弯屈服弯矩在实际中对应的结构反应为截面部分钢筋进入屈服,但整体还处在弹性范围内。这种性能目标阶段处于完全弹性构件与延性构件(产生塑性铰)之间,即认为主塔等重要构件抗震设计要求要高于边墩等桥梁结构中比较容易修复的构件。