应用神经网络技术解决多传感器非线性拟合问题(自动化)
李 莉
(92941部队,辽宁葫芦岛125000)
摘要:针对测量用传感器非线性拟合技术问题,研究采用神经网络技术对传感器非线性误差予以补偿修正,并采用传统数据拟合算法加以比对验证,证明应用神经网络技术可以有效解决多传感器非线性拟合问题。
关键词:神经网络;补偿修正;非线性拟合
中图分类号:TP391 文章编号:1006 - 2394(2016)06 - 0038 - 03
0引言
在雷达跟踪系统中,尽可能消除量测误差的影响是提高跟踪精度的关键之一。由于实际上目标位置的量测以极坐标的形式表示,目标的量测方程在极坐标下是线性的,在笛卡儿坐标系下却是非线性的。与此相反,当目标做线性运动时,跟踪目标的运动方程是非线性的。解决这个问题通常用两种方法,一是首先将极坐标量测转换到笛卡儿坐标系下,再使用线性卡尔曼滤波器( CMKF);另一种方法是使用混合坐标系下的扩展卡尔曼滤波器( EKF)。然而当目标距离较远时,这两种常用的方法都会产生较大的线性化误差。如果能够首先估算出线性化误差,然后在测量方程中对线性化误差进行一定的补偿的话,跟踪精度可以得到有效提高。随着现代信号处理技术的发展,各种新的方法不断出现,神经网络法则不必建立方程,直接通过标定数据进行网络训练即可。对此,本文采用BP神经网络法对测量数据进行拟合,实现数据采集与测试系统的非线性补偿,并结合某功率传感器实例与最小二乘法的拟合结果进行了比较。
1 BP神经网络介绍
人工神经网络是一门新兴交叉学科,在自动控制、模式识别等领域得到了广泛应用。实际应用中的人工神经网络模型大部分采用BP神经网络(Back Propaga-tion Neural Network)。BP算法由两部分组成:信息的正向传递与误差的反向传播。在正向传播过程中,输入信息从输入经隐含层逐层计算,传向输出层,每一层神经元的状态只影响下一层神经元的状态。如果在输出层没有期望的输出,则计算输出层的误差变化值,然后转向反向传播,通过网络将误差信号沿原来的连接通路反传回来,修改各层神经元的权值直至达到期望目标。BP学习规则:调整网络的权值和阈值减小网络误差的平方和最小,这是通过在最速下降方向上,不断地调整网络的权值和阈值来达到的。含有一个隐含层BP神经网络的拓扑结构如图1所示。
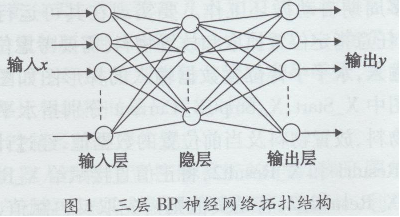
BP模型由具有多个节点的输入层、隐层和多个或1个输出的输出层组成,每个节点为1个单独的神经元,相领两层间单向连接。节点之间的传递函数为S型函数,即:

定来确定函数中的参数值。基于神经网络的回归分析,是将这些样本数据,交给网络学习,根据全局误差极小来判定学习完成,从而确定网络结构参数。其原理是一致的,只是基于人工神经网络的回归用更复杂的表达方式,但同时,它也可以解决更复杂的问题。
2 BP神经网络非线性数据拟合应用实例
表1为某传感器的标定数据,由于器件的非线性,使得传感器实测数据呈非线性,传统的回归是依据测量值寻找近似的函数关系。

由于隐层神经元的激活函数为S型函数的饱和值为0、1,所以数据在提交神经网络处理之前,先按式(3)进行归一化。

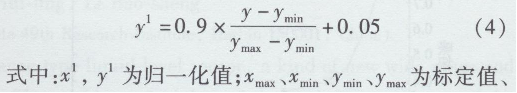
传感器测量值的最大、最小值。归一化后得到的神经网络输入输出标准样本库如表2所示。

标准的BP算法上是一种简单的快速下降静态寻优算法,在修正w(k)时,只是按照k时刻的负梯度方向进行修正,而没有考虑到以前时刻的梯度方向,从而常常使训练过程发生振荡,收敛速度缓慢。在设计中,采用了隐层神经元激活函数定为tansig函数,输出层神经元激活函数为线性函数,算法使用MAT-LAB神经网络工具库中提供的Levenberg-Marquardt
学习算法。在训练过程中,以标定功率的归一化值作为网络的输入,以传感器的实测值的归一化值作为网络的输出,对网络进行训练。使用MATLAB神经网络工具箱仿真,学习训练298次,残余误差为1. 022×10-6。随着神经网络学习时间的延长,神经网络回归拟合剩余标准差不断减小,图2是网络训练误差变化曲线,可见网络训练收敛速度很快。
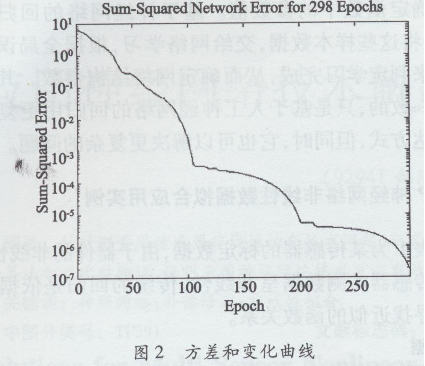
表3是基于BP神经网络数据拟合和基于最小二乘法数据拟合结果比较。
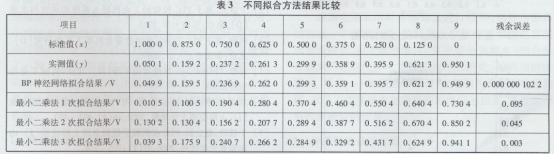
图3是BP神经网络输出的拟合曲线,图4、图5、图6是最小二乘法1次、2次、3次拟合结果的拟合曲线。可见在标定点上,BP神经网络可以很好地拟合标定数据。神经网络回归的剩余标准差小于传统回归方法的剩余标准差,图形曲线和表中的数据也说明了这一点。
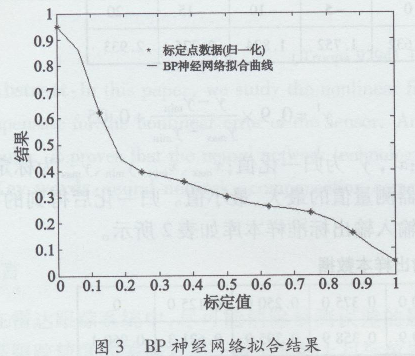
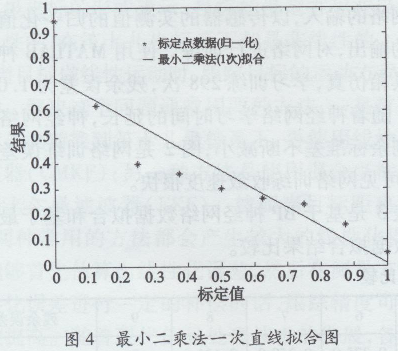
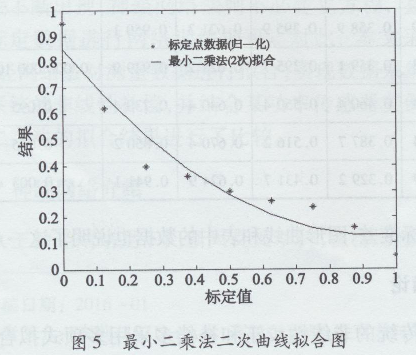
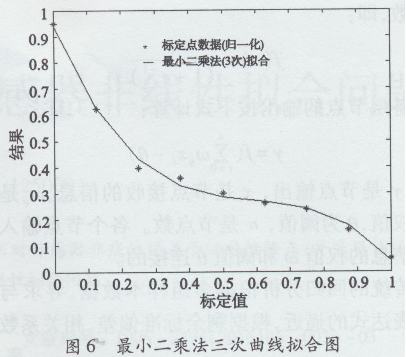
3结论
传统的非线性校正和补偿多采用多项式拟合,本文采用神经网络的拟合技术来修正补偿非线性对传感器输出结果的影响,结果表明该方法能有效地改善传感器和测试系统输出的线性,提高测量的准确度。