大跨径曲线刚构桥转矩调整方案探讨

 王思伟

 （湖南中大设计院有限公司  长沙410075）

摘要  以36 m+60 m+36 m悬臂施工刚构桥(曲线半径300 m)为研究对象，采用MidasCivil有限元分析程序，通过分析全桥转矩成因，结合预应力产生转矩与恒载转矩始终相反的特点，通过改变预应力布置形式，主动调整全桥转矩分布。研究表明：预应力采用不对称布置或不对称张拉力能主动调整一部分转矩。

关键词  曲线刚构桥  转矩调整  预应力  转角

 目前对曲线桥的研究大多集中于等截面连续梁和简支箱梁，而对于挂篮施工的大跨径曲线刚构桥的预应力设计研究并不多见。本文以张家界市白马泉高架桥36 m+60 m+36 m刚构桥（曲线半径为300 m）为研究对象，通过改变预应力的布置方案来减小恒载转矩，提出了有利于主动调整全桥转矩分布的预应力布置方案。

1工程概况

张家界市白马泉高架桥主桥跨径组成为36m+60 m+36 m，右幅桥宽11.0 m。箱梁顶宽11.0 m，底宽6.0 m;支点梁高3.8 m，跨中梁高2.0 m，箱梁梁高按2次抛物线变化；上部结构按A类预应力混凝土结构设计，采用纵、竖双向预应力体系。主墩为矩形截面单肢薄壁墩，墩高分别为14.5 m和16 m。该桥采用悬臂浇筑法施工，先边跨后中跨的合龙顺序。O号块节段长12 m，施工阶段最大悬臂长29 m，边、中跨合龙段长均为2m。桥梁立面图见图1，横断面布置图见图2。

2有限元建模分析

本桥结构扭转跨径对应的圆心角为11. 46。，根据国内外相关研究表明，圆心角大于10度时应按弯桥计算。本文以研究箱梁结构的转矩调整方案为主，采用六自由度三维空间梁单元可以合理模拟桥梁结构中的扭转刚度，计算转矩变化。具体建模如下：采用MidasCivil有限元软件进行计算，主梁采用变截面空间梁单元模拟，主墩采用一般空间梁单元模拟，预应力束采用施加预应力荷载模拟；施工过程中节段湿重、挂篮重量采用节点力和节点弯矩模拟。桥梁模型共划分71个节点，60个单元，计算模型见图3。

3全桥转矩分析

 施工阶段由于节段恒载重心横桥向偏离桥墩中心越来越远，因此节段自重产生转矩，使箱梁向曲线内侧偏转。挂篮等施工荷载同样产生向内侧的转矩。而内侧花槽、人行道系荷载大于外侧的二期恒载，也产生向内侧的转矩。但预应力产生与恒载反方向的弯矩，部分弯矩转化成转矩，刚好与恒载转矩相反。

经过计算，全桥转矩分布及各荷载工况的转矩分布见图4～6。

 结果表明，转矩主要由恒载和预应力荷载产生，恒载在箱梁中支点根部产生的转矩最大，最大转矩为6 522 kN．m。钢束产生的转矩（包含钢束次效应）同样在箱梁根部最大，转矩为1 525kN．m。恒载产生的转矩是不可能改变的内力，而预应力则是一个可变的外加荷载，既然预应力荷载可部分抵消恒载转矩，那么要减小全桥的转矩分布，可从施加预应力钢束荷载角度人手。

4预应力调整转矩方案

 对于等截面的曲线箱梁桥，常用通过支座预偏心的方式主动调整转矩，在工程中已得到广泛的应用。但对于大跨径曲线刚构桥，墩梁是固结的，因此要主动调整转矩，则需曲线内、外侧钢束产生的力偶不对称来调整转矩。

4.1方案一。腹板束采用外大内小布置

 箱梁产生扭转的根本原因是内外侧腹板的剪力不相等，外侧腹板剪力大于内侧腹板剪力，而使箱梁向内侧扭转。原设计方案内外侧腹板束为15fps15.2钢绞线，现将内侧腹板束调整为13Qs15.2，外侧腹板束调整为17Qs15.2，使内侧腹板钢束竖向分力大于外侧，从而减小恒载转矩。

方案一全桥总转矩对比图见图7。

 由图7可见，因采用外大内小的腹板束能产生最大转矩达2 530 kN．m，对恒载转矩有较大的抵消作用。原设计方案最大转矩5 583 kN．m，方案一调整后最大转矩4 010 kN．m，减小幅度达28.1%。

经计算，原设计方案与方案一抗弯承载能力计算结果见表1。

 由表1可见，箱梁抗弯承载能力略有增加，边跨跨中增大0. 58%，中支点增大0.62%，中跨跨中增大0. 58%。按方案一调整后箱梁抗剪承载能力、最大拉应力、压应力，与原方案变化幅度很小，均满足规范要求。

箱梁在弯扭作用下，会产生扭转位移，经计算，原设计方案与方案一的转角位移计算结果对比表见表2。

 由表2可见，边支点和边跨跨中截面转角位移基本没变化，原因是边支点到边跨跨中截面无腹板束，这个区段腹板束产生的转矩很小。而边跨1／4截面转角减小了36.9%，中支点截面转角减小了9. 8%，中跨1／4截面转角减小了21.8%，中跨跨中截面转角减小了13. 7%，而转角减小可显著减小箱梁的横向扭转应力。

4.2方案二。内外侧顶板及腹板束采用不同张拉力

预应力荷载总的效应可分解为竖向力、径向力、轴向力，轴向力不产生转矩，而内外侧径向力始终不能平衡，能使箱梁产生扭转，因此可主动调整内外侧的张拉力，使径向力产生转矩才主动调整恒载转矩。原设计方案钢束张拉控制应力为0. 75，pk，现保持内侧顶板及腹板束张拉控制应力不变，内侧顶板及腹板束张拉控制应力调整为0. 65 fpk。方案二全桥总转矩对比图见图8。

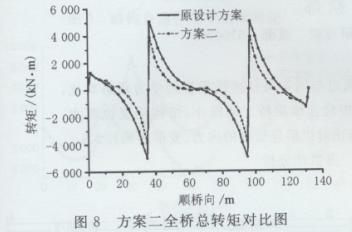
由图8可见，因顶板及腹板束采用不同张拉力钢束能产生最大转矩达2 662 kN．m，对恒载转矩有较大的抵消作用。原设计方案最大转矩5 583 kN．m，方案二调整后最大转矩为3 889kN．m，减小幅度达30. 3%。

经计算，原设计方案与方案二抗弯承载能力计算结果见表3。

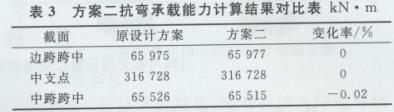
 由表3可见，箱梁抗弯承载能力略有变化，边跨跨中和中支点基本没有变化，中跨跨中减小0. 02%。按方案二调整后箱梁最大拉应力、最大压应力与原方案略有变化，但仍满足规范要求。

经计算，原设计方案与方案二的转角位移计算结果对比表见表4。

 由表4可见，边支点和边跨跨中截面转角位移变化较小。而边跨1／4截面转角减小了25.0%，中支点截面转角减小了8.2%，中跨1／4截面转角减小了24.1%，中跨跨中截面转角减小了13. 7%。

5结论

 (1)采用不对称腹板束的布置形式和内外侧钢束采用不同张拉力构成预应力荷载偏心的方案，能够有效地调整全桥转矩分布，使箱梁受力更加合理，可供类似桥梁结构设计参考。

 (2)2种调整转矩方案都能一定程度地减小全桥转矩分布，显著减小箱梁转角位移，但承载能力和应力略有变化，设计时应结合结构尺寸、应力、承载能力等综合考虑调整幅度，确保主梁各项指标满足规范要求。