论文导读:以植入SMA的航天器的挠性帆板为研究对象,建立了其动力学模型及主动振动控制方程。编制程序对植入SMA丝的帆板在受迫振动情况下的最优主动控制进行了计算,并对结果进行了分析。仿真结果表明,这样的控制规律有效抑制了帆板的振动。
关键词:挠性帆板,最优主动控制SMA,振动抑制
1.引言
新一代航天器的突出的特点是具有大型的挠性附件(包括太阳帆板、天线等)。在航天器的机动过程中, 航天器中心刚体和挠性附件之间存在着强烈的刚挠耦合, 会导致这些挠性结构的持续振动,又由于太空无大气,不存在空气阻尼,挠性附件的振动衰减缓慢。降低挠性结构的振动的最有效的方法是近年来发展起来的主动控制技术。SMA所特有的不同与传统功能材料的力学特性和形状记忆效应,使得其具有对环境条件的感知功能和对系统的驱动功能,可用作自适应结构的主动元件。因而在实际应用中常将SMA丝或颗粒埋入树脂、金属及复合材料的基体中,经过细观力学原理设计制成具有分布式和驱动器功能的智能复合材料,来实现对结构力学行为的主动控制[1]。本文利用SMA丝在约束条件下改变其温度[2][3],可以产生很大恢复应力的特点。将SMA丝植入帆板中,形成SMA驱动器,采用经典线性最优控制有效抑制了帆板的小幅度振动。
2. 嵌入形状记忆合金丝复合材料梁的材料参数
带有太阳帆板的航天器可以简化为中心刚体和固连在刚体上太阳帆板(可以看成挠性梁)构成。在嵌入形状记忆合金丝复合材料梁中,SMA丝沿梁的轴线方向铺设,如图1所示。

图1 嵌入SMA丝复合材料梁的代表性结构单元
用下标“u”表示与基体相关的量,“v”表示与形状记忆合金丝相关的量,“1”方向(x方向)表示SMA丝的方向,“2”方向(Y方向)表示SMA丝的横向,与嵌入形状记忆合金丝后复合材料梁相关的量不用下标。嵌入形状记忆合金丝复合材料梁中,基体所占的体积含量比为 , SMA丝所占的体积含量比为
, SMA丝所占的体积含量比为 ,则
,则
 ,
, (1)
(1)
式中 为复合材料梁横截面的面积,
为复合材料梁横截面的面积, 和
和 分别为基体和SMA丝在横截面上所占面积,
分别为基体和SMA丝在横截面上所占面积,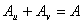 。按照文献[36]的方法,由复合材料混合率公式[89,90]可得到均匀嵌入形状记忆合金丝复合材料梁的材料参数:
。按照文献[36]的方法,由复合材料混合率公式[89,90]可得到均匀嵌入形状记忆合金丝复合材料梁的材料参数:
 (2)
(2)
用上标“*”表示该量与SMA的本构特性有关。
3.挠性帆板的动力学模型
图2所示为近似带有挠性附件的航天器模型,它是由半径为r中心刚体和均匀固连在刚体上太阳帆板(可以看成挠性梁)构成。其中悬臂梁上植入了形状记忆合金丝。相对转动角即姿态角 。
。 表示为外部控制力,其中任意点
表示为外部控制力,其中任意点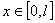 的变形为
的变形为 。主体转动惯量为
。主体转动惯量为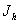 ,固支点到中心o的距离为r。
,固支点到中心o的距离为r。


图2 挠性航天器的结构示意图图3 帆板侧面图
由图3可以看出任意时刻控制力矩。 的大小为
的大小为
 (3)
(3)
其中 ,
,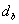 分别为SMA驱动器A, B到帆板中性轴的距离,
分别为SMA驱动器A, B到帆板中性轴的距离,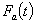 ,
, 分别为t时刻SMA上下驱动器中所有SMA丝拉力的合力,
分别为t时刻SMA上下驱动器中所有SMA丝拉力的合力, ,
, 。
。 ,
,  分别为第i和第j根SMA丝的截面积,
分别为第i和第j根SMA丝的截面积, ,
,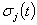 分别为第i和第j根SMA丝t时刻的应力。
分别为第i和第j根SMA丝t时刻的应力。
当采用有限元法时,图2所示有n个自由度的帆板的运动方程为[5]
 (4)
(4)
式中, 表示挠性变形对时间的偏导,即
表示挠性变形对时间的偏导,即 ;
;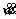 表示挠性变形对时间的二次偏导,即
表示挠性变形对时间的二次偏导,即 ;
; 为嵌入形状记忆合金丝帆板的质量矩阵;
为嵌入形状记忆合金丝帆板的质量矩阵; 嵌入形状记忆合金丝帆板的阻尼矩阵;
嵌入形状记忆合金丝帆板的阻尼矩阵; 分别为嵌入形状记忆合金丝帆板的刚度矩阵;
分别为嵌入形状记忆合金丝帆板的刚度矩阵; 为nXm维控制装置位置矩阵,当第i个自由度上装有第j个控制装置时,
为nXm维控制装置位置矩阵,当第i个自由度上装有第j个控制装置时,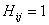 ,其余元素为0;
,其余元素为0; 为外扰力的位置矩阵,在这里
为外扰力的位置矩阵,在这里 ,
,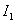 为单位列向量。
为单位列向量。
与式(4)相对应的2n个自由度的状态方程为:
 (5)
(5)
式中,z为 维状态反应向量,
维状态反应向量, ;
; 为
为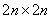 维系统矩阵,
维系统矩阵,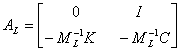 ;
; 为
为 维控制装置位置指示矩阵,
维控制装置位置指示矩阵, ;
;
 为表示外扰力作用的
为表示外扰力作用的 维向量,
维向量, 。其中O、
。其中O、 分别为n维零矩阵和n维单位矩阵。
分别为n维零矩阵和n维单位矩阵。
4.最优控制算法
式(5)为帆板的动力学方程,主动控制中,关键问题是如何确定控制力向量 为1维控制力向量,
为1维控制力向量, 按式(3)计算;
按式(3)计算; 为1外维扰力向量。而主动控制算法是确定控制力的基础,它的目的是使主动控制系统在满足其状态方程和各种约束的条件下,选择合适的增益矩阵,寻找最佳的控制参数,使系统达到较好的性能指标,实现对结构的最佳控制。
为1外维扰力向量。而主动控制算法是确定控制力的基础,它的目的是使主动控制系统在满足其状态方程和各种约束的条件下,选择合适的增益矩阵,寻找最佳的控制参数,使系统达到较好的性能指标,实现对结构的最佳控制。
对于状态方程(5),COC算法采取如下的二次型目标函数:
 (6)
(6)
其中,t0为控制开始的时间;tf为控制终止的时间;P是状态向量权矩阵,为2nx2n维半正定矩阵;L是控制力向量权矩阵,为rxr维正定矩阵。
根据Hamiltonian极值原理,在式(6)的约束下,极小化式(6)所定义的目标函数,可得到COC的闭环控制的最优控制力为[6]
 (7)
(7)
其中, 为反馈增益矩阵,
为反馈增益矩阵, 为Riccati矩阵,有下列微分方程决定,
为Riccati矩阵,有下列微分方程决定,
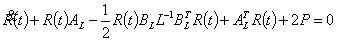 (8)
(8)
大量的计算经验表明,矩阵 在[t0,tf]内的很大一段时间间隔内都是常数矩阵,只是在接近tf的很短的一段时间间隔内迅速趋于零.因此,式(8)退化为非线性矩阵方程,
在[t0,tf]内的很大一段时间间隔内都是常数矩阵,只是在接近tf的很短的一段时间间隔内迅速趋于零.因此,式(8)退化为非线性矩阵方程,
 (9)
(9)
与此对应的控制为 (10)
(10)
将上式代入帆板运动方程得到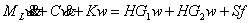 (11)
(11)
其中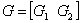 。
。
5.计算程序及算例分析
为说明前述的控制方法的有效性,编制了MATLAB程序对一帆板受迫振动时的主动振动控制进行了计算机模拟。帆板的尺寸为长350mm,宽25mm,高1mm。本文选用的SMA的直径为0.2mm,初始马氏体百分含量为30%,初始应变为2%,环境温度20℃,、。在本例中,每个SMA驱动器由4根SMA丝组成,每个SMA丝的编号如图3所示。
在本文中,帆板固定端输入的载荷为频率为3.18Hz的余弦受迫荷载。图4为有控和无控情况下的梁端位移时程曲线。其中虚线表示无控时,实线表示有空时。当无控时,帆板端的最大位移为10.2mm,当采取主动控制时,帆板端的最大位移减小到了0.43m,减小了95.8%,主动控制有效地抑制了帆板的振动。

图4 受迫载荷下有空和无控时的位移时程曲线
6.结论
在航天器的机动过程中,利用本文设计的SMA驱动器,可以实现帆板的最优主动控制,有效地减小帆板的振动,从而保持机动过程平稳,并迅速实现高精度姿态定位,改善系统的性能。
参考文献:
[1]杨庆生.智能复合材料的热力学特性[J].固体力学学报,1996,17(4):339-342
[2]王军, 郦正能, 叶宁.形状记忆合金智能结构的主动振动抑制研究[J].航空学报,2002,23(5):427-430.
[3]刘建涛.应用形状记忆合金(SMA)的主动结构控制研究[D].天津,天津大学硕士学位论文.
[4]LiangC,Rogers CA .Design of shape memory alloysprings with applications in vibration control[J].Journal of Vibration,Acoustics,Stress,andReliability in Design,1993,115(1):129-135
[5]王勘成,邵敏.有限单元法基本原理和数值方法(第二版) [M].北京:清华人学出版社,1997
[6]YangJ N.Application of optimalcontrol theory to civil engineering structures[J].ASCE, 1995,101 (EM6):819-838