原状冻土Ⅱ型非线性断裂韧度实验测试概述

论文导读:：由于原状冻土处于自然状态下，其本构关系及水分、温度的分布符合实际状态，而且其实际破坏形式往往是非线性的剪切破坏，所以本文采用了非线性冻土断裂实验模型，对自然状态下的原状冻土进行了断裂破坏实验，着重对Ⅱ型断裂（剪切）破坏的四点弯曲直裂纹试样进行了实验研究。实验过程中改造了四点弯曲实验台，采用着色法测量预制裂纹尺寸。实验原理采用基于能量平衡的方法，利用数据采集系统分别测出了原状冻土四点弯曲试样加力点处位移与力的关系曲线以及相应的非线性参数，推导出裂纹扩展非线性能量释放率计算公式，当试样达到承载极限状况时测试出Ⅱ型断裂试样非线性断裂韧度。同时，提出了修正因子计算非线性断裂韧度的方法，将能量方法测试结果与修正因子方法结果进行了对比，二者基本是一致的。以上提出的冻土Ⅱ型断裂非线性断裂韧度测试方法，及获得的非线性断裂韧度测试结果，为非线性理论研究和工程应用提供了依据。
论文关键词：原状冻土，非线性断裂韧度，实验研究

　　1.前言
　　 冻土作为地基基础材料，在上部建筑物荷载作用下，其受力破坏的基本形式是剪切破坏[1]，其强度准则即为众所周知的莫尔－库仑准则，已被广泛应用在冻土地基基础设计中。近年来在开展常规的强度理论研究的同时，相继开展断裂力学、损伤力学等的研究，其中在断裂力学研究方面取得了长足进展[2~4]。用断裂力学理论研究冻土的剪切破坏，即为冻土材料Ⅱ型断裂问题，它涉及了Ⅱ型断裂强度因子的计算和Ⅱ型断裂韧度的测试问题。冻土材料对温度、内部组织及时间因素的改变非常敏感，是一种性质极不稳定的特殊材料，对金属材料、混凝土材料及岩石等的比较成熟的断裂韧度测试方法[5~7]，对冻土材料均不是完全适用的，必须建立考虑冻土特性的测试方法。从冻土工程实际出发，首先应考虑的是冻土非线性特征，其次应考虑冻土在冻结过程中其组构不被破坏，基于以上出发点实验研究，确立了本文的研究宗旨：测定原状冻土在剪力作用的非线性断裂韧度。本文给出了Ⅱ型断裂非线性断裂韧度测试基本原理和方法；进行了原状季节冻土的现场测试；给出了原状冻土Ⅱ型非线性断裂韧度测试结果。为进一步开展冻土非线性理论研究和工程应用提供了依据。
　　2.冻土非线性断裂韧度测试原理和方法
　　研究表明，冻土的破坏可分为脆性和塑性性质，在特定的条件下，如低温、高速率以及粗颗粒冻土破坏时呈脆性状态，其特征是应力－应变关系基本是线性的，破坏时有断裂面且有裂纹发展的痕迹并呈严重破碎状，在这种情况，线弹性断裂力学理论是适用的。但是在更一般情况，冻土的破坏通常都是非线性的，这种情况线弹性断裂理论是完全不适用的，必须研究冻土的非线性断裂破坏特征和性质。因此，冻土非线性断裂韧度的测试是研究冻土非线性破坏性质的重要内容之一。
　　2.1基于能量理论的非线性断裂韧度测试方法
　　冻土材料在外荷载作用下，冻土中的微裂纹发展并形成微裂纹损伤区，最后形成宏观裂纹，在这个过程中，外力做功为，假定它全部转化为材料内的应变能（弹性应变能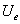及塑性应变能），而微裂纹损伤区形成及宏观裂纹形成需消耗能量为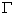，由贮存的应变能来提供，从能量平衡的角度（无热量损失）则有：
　　 （1）
　　当式（1）的能量平衡达到极限状态时：
　　（2）
　　式中 即为非线性能量释放率的临界值，也称为非线性断裂韧度。
　　以Ⅱ型断裂的四点弯曲试样为例（见图3），说明非线性断裂韧度的测试方法期刊网。在加载过程中测试载荷和加力对应点位移，得到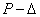曲线，如图1所示。这条曲线的非线性特征可由三个参数来描写：
　　 　（3）
　　式中的是曲线中直线段的斜率，是裂纹长度的函数，有：
　　　 　（4）
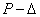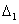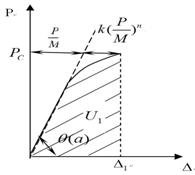
　　，是材料常数，和，同样由实验确定。由曲线可知，当位移达到时，应变能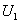　（包括弹性、塑性部分）为曲线下的面积，即实验研究，对任意的则有：
　　　 （5）
　　将（4）代入（5）式得：
　　 （6）
　　
　　
　　将（6）式求导代入（2）式，并考虑到冻土中的微裂纹损伤区刚形成，当不把它作为微裂纹扩展量处理时，外力功不随裂纹变化，则有，于是有[8]：
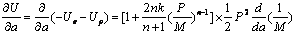　　（7）
　　当载荷达到临界值时，则由上式得到非线性断裂韧度：
　　（8）
　　2．2基于修正因子的非线性断裂韧度测试方法
　　用修正因子法确定非线性断裂韧度可表达为：
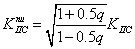　　（9）
　　式中：――Ⅱ型断裂非线性断裂韧度；――非线性修正因子；――Ⅱ型断裂的表观断裂韧度，即未考虑非线性影响的断裂韧度。
　　下面分别说明和的确定方法。
　　（1）表观断裂韧度的测定
　　由四点弯曲试样可知（见图3），在裂纹面的剪切力，因此剪应力可求：
　　 　　（10）
　　相应的应力强度因子为[5]：
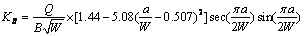　　（11）
　　当达到临界值，也就是载荷达到最大值时，即为：
　　（12）
　　其中：，裂纹长度由着色渗透法确定。
　　（2）非线性修正因子的确定
　　修正因子可从曲线上求得，即在加载时同时测定剪力与裂纹嘴滑开位移，从而获得曲线（图2所示），它与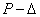曲线一样反映了非线性的信息。
　　
　　

　　从图2可见，图中OA曲线受非线性影响曲线，而OA＇为未考虑非线性影响的曲线，CA为荷载加到时的缷载曲线，斜率为，而曲线的初始斜率为，由CA＇B与CAB的相似关系可得：
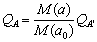　　（13）
　　则定义修正因子为：
　　　 （14）
　　3．试验设计
　　3．1土质及试样制备
　　试样采用沈阳农大实验区的低液限粘土，分析得土壤颗粒成分及物性。冻土断裂韧度采用四点弯曲试样进行试验，并根据冻土特性确定试样尺寸，试样尺寸及其受力如图3所示。试样尺寸：B×W×S=0.1m ×0.1m×0.4m， B为试样厚度，W为试样宽度，S为试样跨距，为预制裂纹，且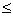0.045m。
　　

　　图3人工切口、预制裂纹的四点弯曲试样尺寸及其受力图
　　Fig.3 the dimension of four-pointbending specimen
　　 由于现场施工取原状冻土难度极大，采用了多种方案，尽量将原状土的内部微细观结构保持完整实验研究，避免对其原有结构产生扰动，取土前先去掉30cm厚的表层土以免由于表层土因受到人为活动而导致土体结构被破坏,影响试验结果，再在取土场人工开挖出长、宽、高分别为80cm×80cm×40 cm见方的较大土块，然后用人工凿取的办法将大土块做成略大于试样尺寸的土块，如图4所示。最后用震动较小的电锯人工切割成满足试验要求的光滑试样。将切好的试样迅速用塑料薄膜包好、编号并测量试样尺寸，放入保温箱中以防止试样温度改变和水分的散失。将其在保温箱中恒温至少24h以上
　　图4 现场取土照片
　　Fig.4 the photo of originalstate frozen soil at field
　　3.2 试样初始裂纹的制作及测量
　　试样的初始裂纹制备是个难点，按照平面应变条件裂纹尖端要求极尖，这对原状冻土来说极其困难，以往方法是先在制备试样时插入楔型木片（涂润滑油便于脱模），以制备初始缺口。在此基础上，再用钼丝锯加工尖裂纹，裂尖半径可达。此方法的缺点是制作的初始裂纹尖端并非极尖，而且这样的初始裂纹并不能准确的反映出试样裂纹尖端扩展的本质。为了改进初始裂纹制备方法，本试验借鉴了岩石断裂力学中所采用的制作方法，先从保温箱中迅速取出一组试样，随后用钼锯锯开初始裂纹，保证裂纹平直，而后将试样放在试验台上先加载到最大力直到试样破坏，可以得到它们的最大值，再根据所得到的计算出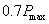值。这样我们就可以将每一个试样预先加载到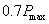值，使其在原有木锯初始裂纹开口的基础上制造出裂纹尖端。这样制作出来的裂纹尖端比传统的方法制作出来的裂纹尖端不仅能够满足按平面应变条件要求的裂纹尖端极尖，而且能够准确的反映出试样裂纹扩展区的实际情况，因此，使试验更复合实际、更具有可靠性。
　　

裂纹长度的测量也是个难点，从前的方法是将试样压断后，在断口平面等间距直接量出三个值后取平均值作为计算裂纹长度，这种做法由于裂纹尖端的模糊不清而存在着很大的误差。为了克服由此产生的误差，我们同样参照岩石断裂测试方法，利用在低温下仍然有较好液性的柴油作为染料，在裂纹切口处均匀喷洒少量柴油，使其均匀沿裂缝下渗直达裂纹尖端，这样一来当试样被压断后实验研究，在断面处可以的看到由于柴油下渗到裂纹尖端而留下的清晰印记，以此为依据，便可以比较准确的测量出裂纹的尺寸了
　　3.3 试验装置
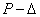　　 本试验对传统的试验装置进行了改造，将三点弯曲试验台倒置悬挂于上端，在下端采用油压千斤顶加力，这样有利于对试样应用着色法测量裂纹尺寸。如图5所示，这样做的好处是使得采用着色法的液体染料能够沿着裂纹扩展方向渗透，并留下清晰的印记，以便于裂纹尺寸的测量。而后利用自动数据采集系统采集数据，绘出及曲线。
　　
　　图5 试验装置照片
　　Fig.5 the photos of experimentalequipment
　　4.试验结果
　　（1）原状冻土试验除了要保持土的细观结构外，还考虑土的冻结历史，可以测试在不同冻结历史条件下的断裂韧度，为此，对当地冬季地温及冻胀量随时间的变化规律进行了测量，进而使试验能够控制在该规律下进行。
　　（2）试样在相同的加载速率、相同的天然含水率为和相同的温度变化规律（与该种土质在实际相同深度处的冻土温度变化规律相同）情况下，可以得到如图8所示的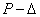曲线图，从图6中可以清楚的看出：荷载在达到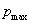破坏之前有明显的塑性变形，说明此种冻土具有明显的弹塑性属性期刊网。 当载荷达到最大值时试样断裂，对于四点弯曲一般断裂时会有一个开裂角，如图7所示，开裂角的角度值列于表1中。
　　 　　
　　

　　（3）当冻深为110cm时，取距表层土60cm深的冻土体，制备Ⅱ型裂纹试样，控制试验温度为-3.1℃,含水量为17%，获得非线性断裂韧度值。如表1所示。这个结果相应于土体从冻结开始到2005年1月20日的冻结历史。
　　表1 原状冻土的Ⅱ型非线性断裂韧度试验计算结果
　　Tab.1 theexperimental results of nonlinear fracture toughness for frozen soil
　　

（3）按修正因子法计算结果
　　 对上述试样同时做出了曲线，并用修正因子法计算出非线性断裂韧度，结果列于表2中。
　　表2　原状冻土的Ⅱ型非线性断裂韧度试验计算结果
　　Tab.2 the calculate value ofnonlinear fracture toughness forfrozen soil
　　

非线性断裂韧度与非线性能量释放率值都是表征冻土材料的非线性特征，二者应有对应关系。对于线弹性情况，能量释放率与断裂韧度有如下关系：
　　（15）
　　假定上述关系对非线性情况也同样成立，若取－3℃时的＝400MPa，＝0.25，则将换算为实验研究，并与实测比较，除两个试样误差较大，其余的基本是一致的，其结果列在表3中。
　　表3　将换算为与实验测得的相对比的结果
　　Tab.3 　the comparisonbetween the value of calculatedform andthe value of formthe experiment
　　

5.结论
　　（1）本文的研究是针对沈阳地区的土质所进行的原状冻土断裂力学试验。由于冻土工程中经常发生剪切的破坏形式，所以着重对Ⅱ型断裂（剪切）破坏的四点弯曲直裂纹试样进行了实验研究。并用染色剂对裂纹尺寸采用着色法观测。通过对当地土质进行分层冻胀量的观测，得出不同埋深处的冻胀量、冻融的关系，并以此来严格控制试样制作、试验时的温度，对原状冻土的Ⅱ型非线性应变能量释放率和非线性断裂韧度进行测试研究，这是对原状冻土非线性断裂力学试验的进一步的探索和尝试，它为今后进一步的研究工作奠定了基础。
　　（2）本文给出了关于冻土的两种非线性断裂韧度测试方法的结果，分别是基于能量平衡的测试方法和基于修正因子的测试方法，在实际工程应用中，可以相互参照，灵活运用。
　　 （3）由于原状冻土完全处于自然状态下，其结构及内部缺陷随机性较大，实验过程中所采集的数据有一定的离散性，因此需要更多的试样和大量的实验数据，并进行统计分析，使结果与实际情况相符。

参考文献
[1]吴紫汪，马巍.冻土强度与蠕变[M]。兰州：兰州大学出版社，1994。(WuZ W, Ma W. Frozen soil strength and creep[M]. Lanzhou, Lanzhou UniversityPress.)
[2]李洪升，朱元林.冻土断裂力学及其应用[M]。北京：海洋出版社，2002.（Li H.S., Zhu Y.L, FractureMechanics of Frozen Soil and Its Application[M]. Beijing, China Ocean Press. 2002.）。
[3]李洪升，刘增利，朱元林。冻土断裂韧度测试的理论和方法[J]。岩土工程学报，2000，22（1）：61-65。(Li H.S., Liu Z L, Zhu Y.L. Theory and methods on testsof the fracture toughness K_(Ⅰc) of frozen soil[J]. Chinese Journalof Geotechnical Engineering, 2000，22（1）：61-65.)
[4]Wang Yuedong，Li Hongsheng，Liu XiaoZhou. The experiment research of nonlinear mode Ⅱ fracturetoughness for the original state frozen soil，the 11thexperimental mechanics conference of china，2005：377-386
[5]王铎.断裂力学[M]，南宁：广西人民出版社，1982，74-76。(Wang F. Fracture Mechanics[M]. Nanning: Guangxi PeoplePress.)
[6]Hillerborg.A,modeer.M, Petersson.P.E, Analysis of crack formation and crack growth inconcrete by means of fracture mechanics and finite elements, Cement andConcrete Research, 1976, 773-782
[7]Xu, X-P andNeedleman, A. Numerical simulations of fast crack growth in brittle solids,Journal of the Mechanics and Physics of Solids, Vol. 42, pp. 1397-1434 (1994).
[8]WhittakerB.N., singhand R.N. Sun G. [M]. Rock Fracture Mechanics. Elsevier SciencePublishers B.V. 1992.