作者:张毅
地震易损性评估中存在诸多的不确定性,包括人的认知缺失造成的主观不确定性和地震动、材料属性等客观不确定性。国外学者开展了大量的关于地震易损性评估中不确定性量化与传播研究。研究显示:在地震易损性分析中,较之地震动的不确定性,其他客观不确定性和主观不确性对于实际工程结构的地震易损性影响较小。此外,后两种不确定性分析会使抽样样本空间倍增,以致计算量倍增。因此,在地震易损性评估中可以只考虑地震动不确定性的影响。为了合理地考虑地震动不确定性的影响,Vamvatsikos和Cornell基于弹塑性时程分析系统地提出了增量动力分析( IDA)方法。
工程需求参数( Engineering Demand Parameter,EDP)与地震动强度指标(Intensity Measure,IM)的概率函数关系可以通过对IDA曲线簇进行统计分析获得,在此基础上,可进一步获得建筑结构的地震易损性曲线。国内外学者提出了大量的IDA统计分析方法,但是由于IDA曲线具有“非单调”、“回折”和“平台阶段”等现象,这些方法均有一定的局限性。为了改善这一问题,本文基于贝叶斯理论提出了一种IDA曲线簇统计分析方法,并通过一个3跨3层钢筋混凝土框架算例讨论了所提出方法的优越性。
1 常见的IDA曲线簇统计分析方法
1.1拟合统计方法
拟合统计方法一般是先假设工程需求参数(如最大层间位移角Omax)和地震动参数(如谱加速度Sa)满足一定的函数关系:

式中a,b为常系数。
化简可得:

此时θmax和Sa在对数坐标系中满足线性分布。
假设结构能力参数R和结构响应参数.S满足对数正态分布,则结构的失效概率P可表示为:

式中:ms和Ps分别为结构响应的对数均值和对数标准差;mR和βR分别为结构抗力的对数均值和对数标准差;Φ()为标准正态分布的累积分布函数。
将式(2)代入式(3),便可得到结构失效概率P,即地震易损性。然而,此方法存在以下问题:1)工程需求参数和地震动参数并不一定符合对数线性关系;2)没有通过IDA曲线簇系统地考虑地震动不确定性的影响。
1.2以工程需求参数为变量的统计分析方法
以地震动强度参数( EDP)为变量的统计分析方法是指将地震动强度指标(IM)看作EDP的函数。对于给定的IM =x,EDP满足对数正态分布。此时,便可以通过如图l所示方法在IDA曲线簇中选取统计信息。在IM =x强度的地震作用下结构发生超越某一极限状态LSi的概率,即结构地震易损性,可以通过下式计算:

式中μ和σ分别为对IDA曲线簇统计分析获得的IM =x时EDP的对数均值和对数标准差。
以IM为横坐标,P(EDP>LSi∣ IM=x)为纵坐标,即可绘出极限状态LSi的地震易损性曲线。
此种方法假定建筑结构在给定的地震动强度IM =x作用下的动力响应满足对数正态分布。利用IDA曲线簇结合此假定来考虑地震动不确定性对建筑结构地震易损性的影响。然而,在某些情况下,此方法并不适用。例如图1中,当Sa=0. 6g时,能够得到7组有效的EDP数据,对这7组EDP数据进行统计分析,便可以得到相应的对数均值和对数方差,然后可以按照式(4)进行地震易损性的计算;但是当Sa=1. 2g时,只能取到4组有效的EDP数据,而且Sa=1. 2g横线与另外3条进入平台阶段的IDA曲线没有交点。此时,缺乏3组有效的EDP数据,无法进一步开展统计分析。

1.3以地震动强度参数为变量的统计分析方法
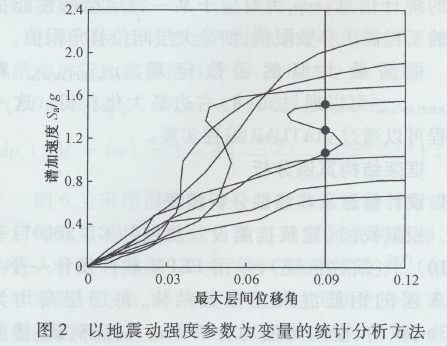
以地震动强度参数为变量的统计分析方法是指将EDP看作IM的函数。对于给定的EDP= LSi,IM满足对数正态分布。则可以对IDA曲线簇开展统计分析,如图2所示。此时,在IM =x强度的地震作用下结构发生超越某一极限状态LSi的概率可以通过下式计算:

式中θ和β分别为对IDA曲线簇统计分析获得的EDP= LSi时IM的对数均值和对数标准差。
虽然此种方法不存在1.2节所述的与IDA曲线没有交点的问题,但是此种方法也存在以下问题:IDA曲线簇并不一定是单调曲线,可能存在“回折”现象。例如图2中,当EDP=0.09时,对于一条IDA曲线能够同时取到3组有效的IM数据。此时便不可以采用此方法进一步展开统计分析。
2 基于贝叶斯理论的IDA曲线簇统计分析方法
2.1贝叶斯推断
贝叶斯理论认为:后验密度等于先验密度与标准化的似然函数的乘积。后验分布f(Θ)可以采用下式计算:

式中:Θ=(θ,σ),代表待定参数;p(Θ)为关于Θ的先验分布;ι(Θ∣y)为考虑数据y后,待定系数的似然方程;c=[f(Θ)ι(Θ∣y)p(Θ)dΘ]-1,为归一化的系数。
所以f(Θ)即包括了关于Θ的先验分布也包括了数据对Θ的影响。当未知系数的先验分布无法确定时,一般采用“无信息化”先验分布,对于Θ的无信息化分布,可以采用Box建议的均匀分布,表达式如下:

2.2统计分析方法
贝叶斯理论能够利用试验数据对事件的概率估计进行修正。本方法主要用于解决以工程需求参数为变量的统计分析方法中IDA曲线与im(某一特定地震动强度指标)没有交点的问题。假设有m条IDA曲线,其中n条与im没有交点,在m-n组交点中最大的工程需求参数为edPmax。依据贝叶斯推断原理,可获得如下似然函数:

式中:p()为标准正态分布密度函数;第一项表示m -n组有交点的统计信息;第二项表示n组没有交点的统计信息;edpi为对应于某一特定结构性能指标的工程需求参数限值,如最大层间位移角限值。
根据最大似然函数定理,μlnEDP∣IM=im和σlnEDPIM=im可以通过式(8)右边最大化获得。这一过程可以通过MATLAB编程实现。
3 框架结构算例分析
3.1设计信息及非线性分析模型
根据我国《建筑抗震设计规范》( GB 500011-2010)(简称抗规),采用PKPM软件设计一个3跨3层的钢筋混凝土框架结构,每层层高均为3. 3m,纵向、横向跨度均为7.2m。设计荷载:楼面恒载为4.0 kN/m2,活载为2. OkN/m2。抗震设防烈度为7度(0. 15g),地震分组为第二组,场地类别为Ⅱ类,结构阻尼比为0. 05。采用的混凝土强度等级为C30,纵筋、箍筋均为HRB335。取出中间一榀框架作为分析的结构模型,柱截面尺寸为450×450,梁截面尺寸为250×500,框架尺寸、截面配筋情况见表1。利用OpenSees软件建立非线性有限元分析模型。梁柱均采用集中塑性铰单元( Beam WithHinges Element),截面采用纤维截面模型(FiberSection)。混凝土材料模型采用Concrete01,钢筋材料模型采用Stee102。

3.2地震波的选取
为了考虑地震的震级、断层距等因素对结构动力响应的影响,根据Sirrion提出地震划分原则,把地震波划分为五大类,见表2。不同的场地土类型对应的地震波剪切波速是不一样的,比如对于美国地质调查局( United States Geological Survey,USGS)中的S2类场地,剪切波速为360~ 750m/s。综合考虑表2中地震波的分类和S2类场地剪切波速的取值范围,在美国太平洋地震工程研究中心强地震动数据库中,在五大类地震波中一共选择15条,每一类地震波为3条,地震波详细信息见表3,反应谱见图3。


3.3工程需求参数和结构的性能指标
结构工程的抗震性能水准主要是通过工程需求参数来表征的,通过定义工程需求参数来表示结构在此方面的抗震性能。目前,常用的工程需求参数为最大层间位移角,其简单适用,操作性强,所以广为采用。简化起见,本算例采用最大层间位移角作为工程需求参数。
在地震易损性分析中,通常将建筑结构在地震作用下发生的破坏分为若干等级,每一个等级对应的状态称为极限状态,亦称性能水准( PerformaceLevel)。美国联邦应急管理署(FederalEmergency Management Agency,FEMA)将钢筋混凝土框架结构的性能水准划分为3类:立即使用(Immediate Occupancy,IO);生命安全(Life Safety,LS);防止倒塌(Collapse Prevention,CP)。对应的最大层间位移角限值,见表4。

3.4 IDA曲线簇
利用第3.2小节选取的15条地震波对设计的3层钢筋混凝土框架结构进行增量动力时程分析,获得IDA曲线簇如图4所示。由图可知,部分IDA曲线存在“回折”现象,以地震动强度参数为变量的统计分析方法显然不适用于此IDA曲线簇的统计分析;当地震动强度参数达到一定的数值时,部分IDA曲线与横线没有交点,显然无法采用以工程需求参数为变量的统计分析方法。

3.5分位线曲线
IDA曲线簇表示结构在不同地震动水平下的动力响应,本质上是一个随机的需求函数,即EDP=f(IM)。通过求取数学特征值(比如标准差、平均值等)可以得到IDA曲线簇的统计特性。分位线曲线是描述IDA曲线簇统计特性的主要表示方法。图5为采用贝叶统计分析方法计算所得分位线曲线。由图可以看出,贝叶斯统计分析方法可以有效地克服以工程需求参数为变量的统计分析方法存在的问题,可以开展高地震强度指标范围的IDA曲线簇统计分析。

3.6易损性曲线
获得IDA曲线簇的平均值和标准差,便可对建筑结构进行地震易损性评估,具体方法如下式:


图6为采用拟合统计方法和贝叶斯统计方法计算所得地震易损性曲线。随着地震强度的增加,结构进入非线性阶段,其动力响应离散性变大。相比贝叶斯统计方法,传统的分析方法无法充分考虑响应数据的离散性。所以在“生命安全”和“防止倒塌”陛能水准的易损性分析方面,拟合统计分析方法会造成较大的偏差。
4 结论
(1)在IDA曲线簇的统计分析中,应尽量直接采用IDA计算结果,不宜进一步对IDA计算结果进行拟合统计,如此可能会造成较大的偏差。
(2) IDA曲线簇具有“非单调”、“回折”和“平台阶段”等复杂现象,从而使得传统统计分析方法的适用范围有较大限制。
(3)利用贝叶斯统计分析方法,可以有效地开展IDA曲线簇统计分析。
5[摘要] 地震易损性分析是评估建筑结构抗震性能的重要手段,增量动力分析又是地震易损性分析的数据基础,其曲线簇的统计分析直接关系着地震易损性分析结果。然而,由于增量动力分析曲线存在“非单调”、“回折”和“平台阶段”等复杂现象,常见的统计分析方法均存在一定的限制。基于贝叶斯理论,提出了一种新的统计分析方法。该方法可以较好地解决由于增量动力分析曲线簇的复杂性而引起的统计问题。最后,利用提出的贝叶斯统计分析方法对一个3跨3层钢筋混凝土框架结构开展了地震易损性分析,表明该方法可以有效地开展IDA曲线簇统计分析。